数学の基礎として、さまざまな物体の面積を求めることがあります。
中でも円柱は比較的問題として取り上げられる形状であり、特にその表面積の計算が出題されることがあります。
ただ、表面積と似た言葉に「側面積」「底面積」などの用語があり、混同する場合があります。
ここでは、円柱の「側面積」「底面積」「表面積」の公式や計算方法について解説していきます。
目次
円柱の側面積の公式と求め方【側面積の単位】
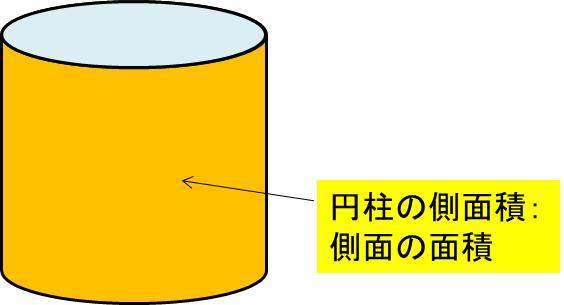
まず、円柱の側面積の定義について確認していきます。言葉からも想像がつくように、側面積とは側面の面積であり円柱では、以下の図の部分の面積に相当するのです。
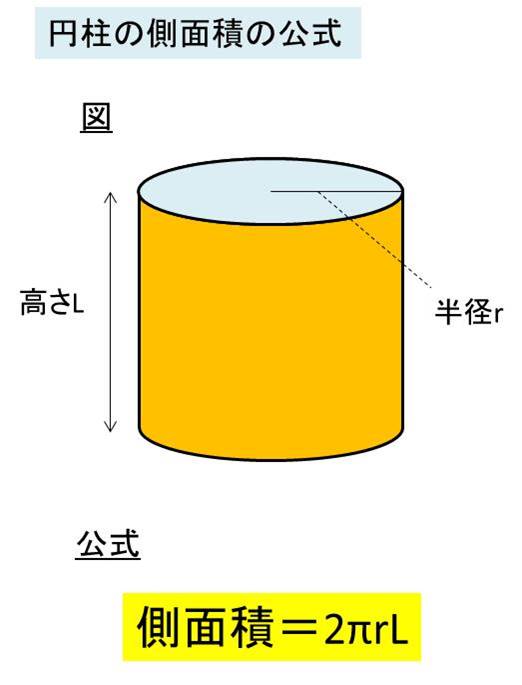
そして、円柱の側面積の公式は側面積=2πrLとなります。ここで、πは円周率、rは底面の半径、Lは高さを表しています。
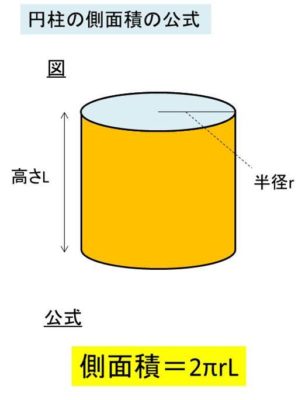
この側面積の計算式の覚え方としては、円柱を帯をあるところで切って、それを広げた長方形になっていると考えるといいです。以下のようなものです。
※
なお、先述のよう側面積は面積の一種であるため、単位には平方センチメートル(cm2)や平方メートル(m2)などを使用します。
円柱の側面積の計算問題を解いてみよう
それでは、理解を深めるためにも円柱の側面積の問題を解いてみましょう。
例題1
半径3cm、高さ5cmの円柱があります。円周率を3.14とした場合の円柱の側面積を計算してみましょう。
解答1
上の側面の面積の公式を利用します。
円柱の側面積=2×3.14×3×5=94.2cm2となるのです。きちんと理解しておきましょう。
円柱の底面積の公式と求め方【底面積の単位】
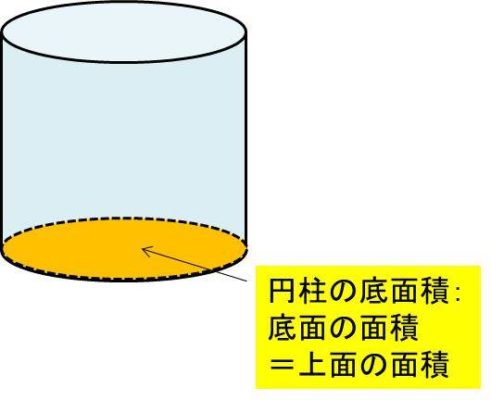
続いて、円柱の底面積の定義について確認していきます。底面積とは、円柱における底の部分の面積であり、円柱のように高さ方向に形状が変化さいない物体では上面の面積と一致します。
そして、円柱の底面積の公式は通常円の面積を求める公式と同様に、底面積=πr^2という計算式となります。ここで、πは円周率、rは底面の半径、Lは高さを表しています。
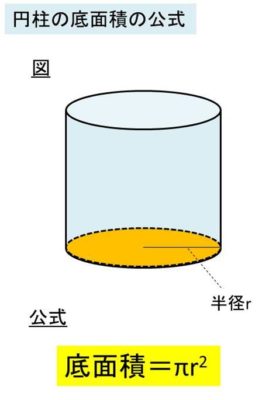
底面積といっても、「単純に円の面積を求めればいい」ということを理解しておきましょう。
底面積の単位は側面積などと同様、平方センチメートル(cm2)や平方メートル(m2)などを使います。
円柱の底面積の計算問題を解いてみよう
それでは、理解を深めるためにも円柱の底面積の計算を行っていきましょう。
例題1
半径4cm、高さ2cmの円柱があります。円周率を3.14とした場合の円柱の底面積を計算してみましょう。
解答1
上の底面の面積の公式を利用します。なお、もし上面の面積を求めなさいと言われても同じ手順で対応するといいです。
よって、円柱の底面積=4×4×3.14=50.24cm2となるのです。きちんと理解しておきましょう。
円柱の表面積の公式と求め方【表面積の単位】
最後に円柱の表面積を意味をみていきましょう。表面積とは、言葉の通り表面にでている部分の面積のことを指します。
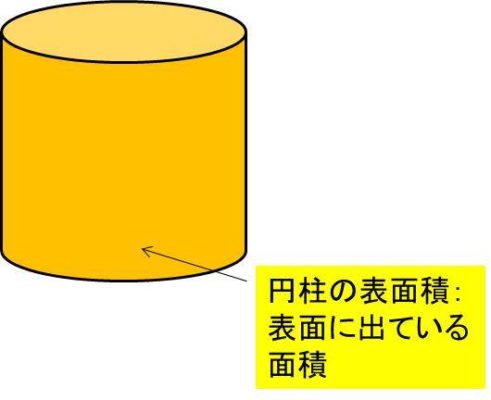
円柱では上で解説した側面積、底面積と上面積を足し合わせたものといえます。ここで、円柱では底面積と上面積は同じであるため、表面積=2×底面積+側面積と表せます。

円柱の表面積を計算式にしますと、表面積=2πr^2+2πrL という計算式となります。ここで、πは円周率、rは底面の半径、Lは高さを表しています。
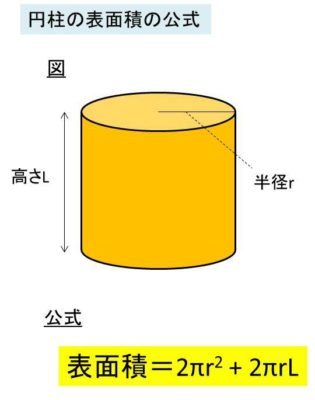
表面積の単位は側面積などと同様、平方センチメートル(cm2)や平方メートル(m2)などを使います。
円柱の表面積の計算問題を解いてみよう
それでは、表面積の扱いに慣れるため、例題を解いていきましょう。
例題1
半径5cm、高さ4cmの円柱があります。円周率を3.14とした場合の円柱の表面積を計算してみましょう。
解答1
上の表面積の面積の公式を利用します。
表面積=2×3.14×4×4+2×3.14×4×5=100.48+125.6=226.08cm2と求められるのです。
これらが、円柱の側面積、底面積、表面積の計算方法です。きちんと理解しておきましょう。
まとめ
ここでは、円柱の側面積、底面積、表面積の公式や求め方、単位について解説しました。
側面積とは側面の面積を表し、底面積とは底面の面積を指し、表面積とは底面積の2倍の数値と側面積を足しあわせたものです。
各々の計算式は、側面積:2πrL、底面積:πr^2、表面積:2πr^2+2πrLで表すことができ、その単位はcm2、m2、mm2などを使います。
たくさん問題を解き、円柱に関する面積の計算をマスターしていきましょう。