数学や算数において、さまざまなパターンの図形の問題が出題されます。中でも円に関する計算問題は多く、各問に対する解き方を学んでおくといいです。
ここでは、「円を半分にした形状である半円」や「4分の1の円(四分円)」の面積を求める方法について解説していきます。
目次
半円の面積の求め方
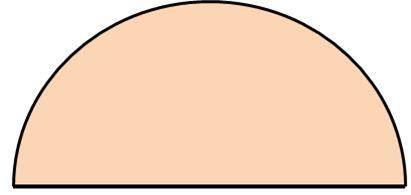
円の中でも半円とは、言葉の通り円を半分に切った形といえ、以下のようなものです。
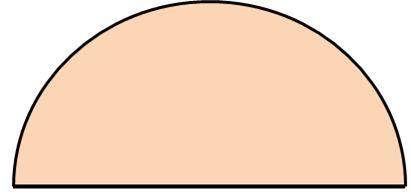
半円は円の面積の半分であるため、「半円の面積=半径×半径×円周率(約3.14)÷2」という公式で求めることができるのです。
以下の通りです。

半円の大きさの考え方はとてもシンプルなので、きちんと理解しておきましょう。
なお、半円の周の長さの求め方はこちらに記載しているので参考にしてみてください。
四分円(四分の一の円)の面積の求め方
同様に、4分の1の円について考えていきましょう。まず、4分の1の円とは以下のような形状をしたものを指します。
そして、半円と同様に円の面積の計算式を4で割ることで求めることができます。

このような公式で半円や、四分円の面積が算出できるのです。
半円と四分円(四分の一の円)の面積の計算を行ってみよう
それでは、これらの円の面積の解き方に慣れるためにも、実際に計算問題を解いてみましょう。
まずは半円から考えていきます。
半円の面積の計算問題
例題
半径5cmの半円の面積はいくらになるでしょうか。円周率は3.14として計算してみましょう。
解答
上の公式にしたがって求めていきます。
半円の面積=3.14×5×5÷2=39.25cm2(平方センチメートル)となります。
四分円の面積の計算問題
続いて、四分の一の円の大きさを求めましょう。
例題
半径3cmの四分円の面積を求めてみましょう。
解答
こちらも上の計算式を元に算出します。
3.14×3×3÷4=7.065cm2と計算できるのです。
まとめ
ここでは、半円、四分円(四分の一の円)の面積の求め方について解説しました。
半円であれば円の面積の半分の数値、四分円の面積であれば円の面積を4で割った値に相当します。
計算式にしますと、「半円の面積:円周率×半径×半径÷2」「四分の一の円の面積:円周率×半径×半径÷4」で求められるのです。
なお、この公式自体を忘れてしまったとしても、半円や四分の一の円の形状をみれば、どのように計算すればいいのか見えてきます。そのため、式の丸暗記というよりも、計算式が出てくる過程を理解しておくことがおすすめです。
円に関する計算に慣れ、算数、数学をより得意にしていきましょう。