数学の問題を解いていると、平方根の計算に出会うことは多いもの。
特に√37のような素数の平方根は、電卓なしでは正確な値を求めにくく、覚え方や近似値の求め方を知っておくと便利です。
受験勉強や資格試験でも頻出するこの数値について、計算方法から語呂合わせまで、詳しく解説していきましょう。今回は37の平方根の値を中心に、実用的な知識をお伝えします。
目次
37の平方根の値はいくつか
それではまず、37の平方根の正確な値について解説していきます。
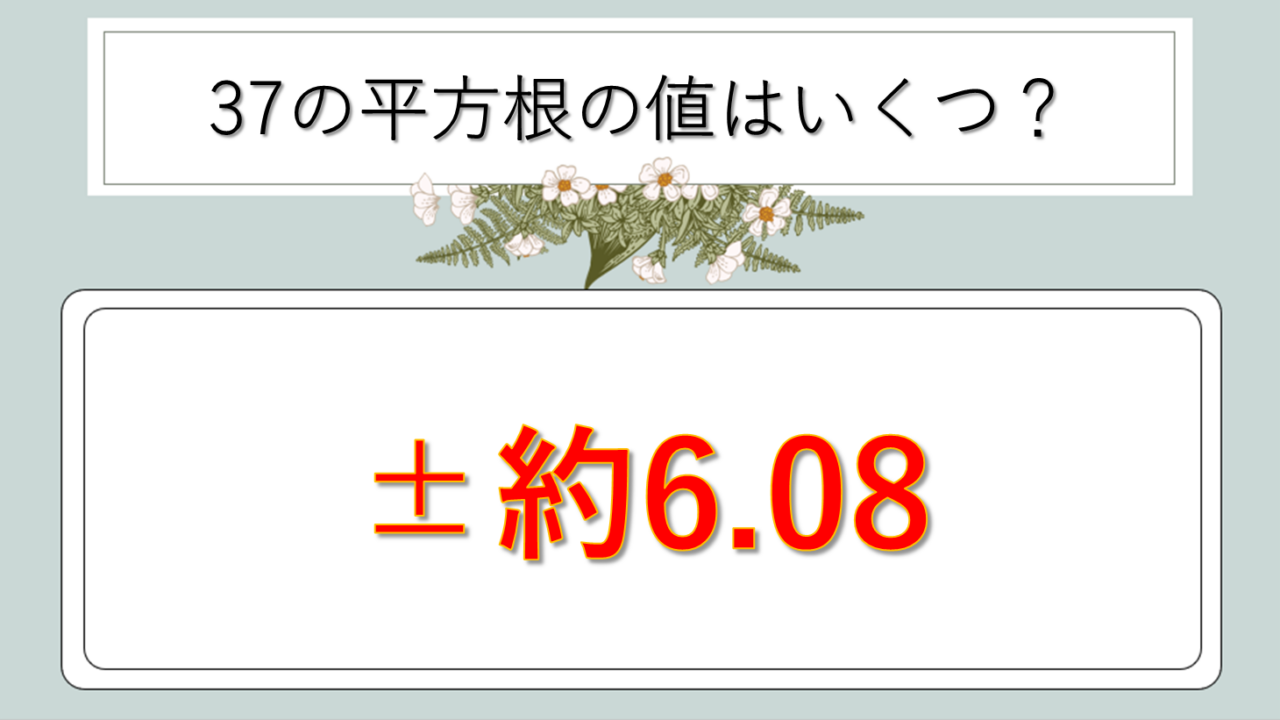
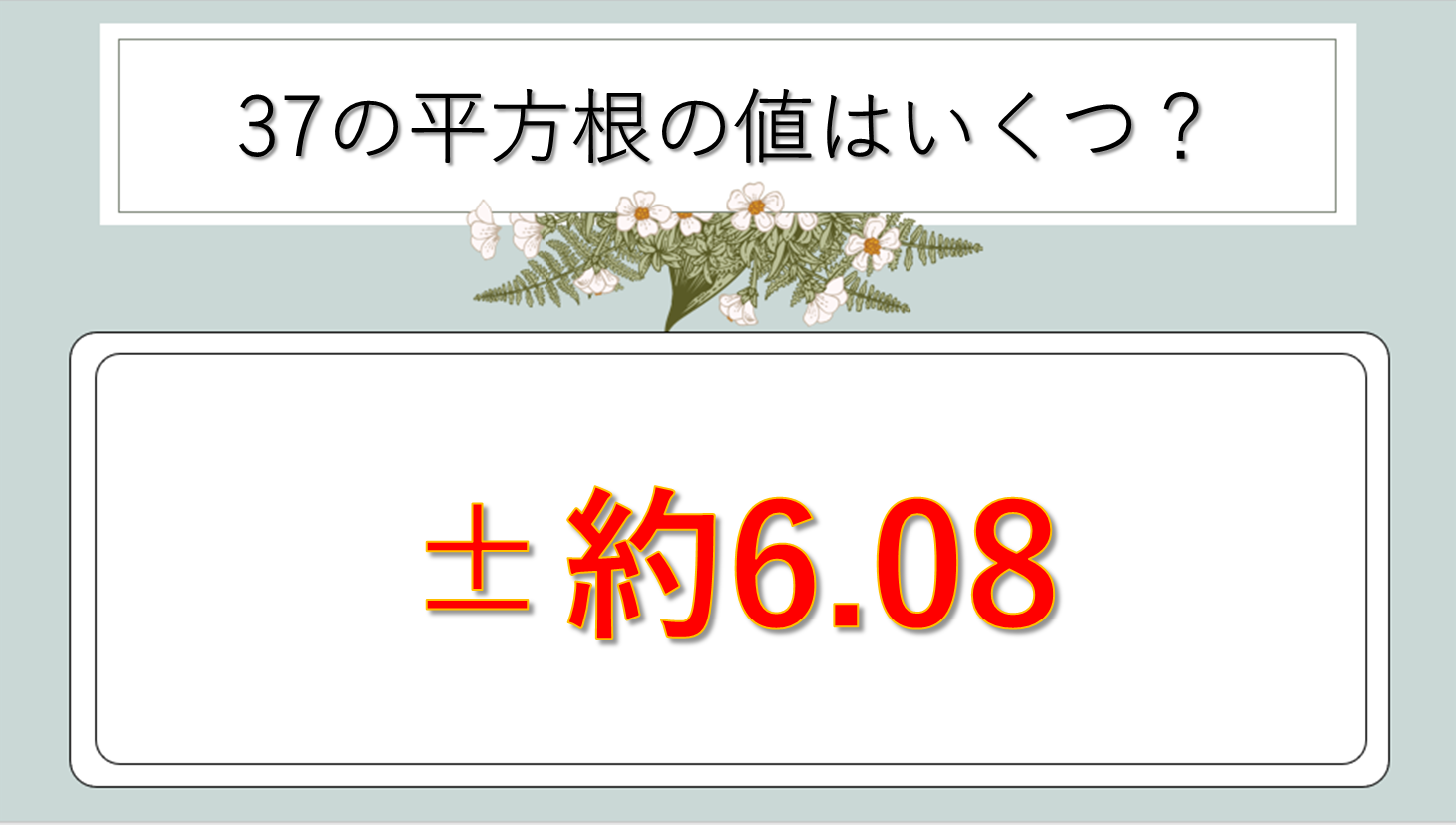
√37は無理数であり、小数点以下が無限に続く数です。電卓で計算すると、次のような値になります。
この数値を見てわかるように、√37は約6.08という値。6と7の間にある数であることは明らかでしょう。
より詳しく見ていくと、小数第一位まででは6.1、小数第二位までなら6.08となります。日常的な計算では、この程度の精度があれば十分なことが多いですね。
ちなみに、√37の2乗が37になることを確認してみましょう。これは平方根の定義そのものです。
当たり前のようですが、この関係性を理解しておくことが、平方根を扱う上での基礎となるのです。
37の平方根の覚え方と語呂合わせ
続いては、37の平方根の覚え方について確認していきます。
数値を丸暗記するのは大変ですが、語呂合わせを使えば記憶に残りやすくなるもの。√37の場合、6.08という近似値を覚えるための語呂合わせがいくつか存在します。
代表的な語呂合わせをご紹介しましょう。
「むれておや」(6.08)
「ろくまるはな」は、6.08の数字をそのまま読んだもの。シンプルで覚えやすいのが特徴です。
もう少し精度を上げて、6.082まで覚えたい場合はどうでしょうか。
このように、必要な精度に応じて語呂合わせを選ぶとよいでしょう。
| 近似値 | 語呂合わせ例 | 用途 |
|---|---|---|
| 6.08 | ろくまるはな | 日常計算・概算 |
| 6.082 | ろくまるはに | やや精密な計算 |
| 6.0827 | ろくまるはなな | 高精度計算 |
語呂合わせは人それぞれ覚えやすいものが違います。自分なりのフレーズを作ってみるのも一つの方法ですね。
37の平方根の近似値の求め方
続いては、37の平方根の近似値を計算で求める方法を確認していきます。
電卓がない状況でも、ある程度の精度で√37を求める方法があります。最も基本的なのは、近い完全平方数を利用する方法でしょう。
まず、37に近い完全平方数を探してみます。
7² = 49
37は36と49の間にあるため、√37は6と7の間の数であることがわかります。さらに、37は36により近いことから、√37は6に近い値だと推測できるでしょう。
より精密に求めるには、線形補間という方法が使えます。
= 6 + 1/13
≒ 6 + 0.077
≒ 6.077
この計算により、実際の値6.082に非常に近い近似値が得られました。
もう一つの方法として、ニュートン法(Newton-Raphson法)があります。これは繰り返し計算によって、より正確な値に近づいていく手法です。
x_{n+1} = (x_n + 37/x_n) / 2
2回目: x₂ = (6.083 + 37/6.083) / 2 ≒ 6.0828
わずか2回の計算で、かなり正確な値が得られることがわかります。この方法は手計算でも実行可能で、精度を上げたいときに便利ですね。
37の平方根を簡単にする方法
続いては、37の平方根を簡単にする方法について確認していきます。
平方根を簡単にするとは、√の中の数を素因数分解して、可能な限り√の外に出すこと。しかし、37は素数であるため、これ以上簡単にすることはできません。
素因数分解を試みてみましょう。
37自身が素数なので、他の因数を持ちません。したがって、√37はこれ以上約分できない形なのです。
参考までに、簡単にできる平方根の例を見てみましょう。
√48 = √(16×3) = √16 × √3 = 4√3
√72 = √(36×2) = 6√2
このように、平方数を因数に持つ場合は簡単にできます。しかし37の場合、そのような因数が存在しないため、√37という形が最も簡単な表現となるわけです。
| 数 | 素因数分解 | 平方根の簡単な形 |
|---|---|---|
| 36 | 2² × 3² | 6 |
| 37 | 37(素数) | √37(これ以上簡単にできない) |
| 48 | 2⁴ × 3 | 4√3 |
37の平方根の計算における注意点
続いては、実際の計算で√37を使う際の注意点を確認していきます。
まず重要なのは、有理化の処理です。分母に√37が来る場合、有理化することで計算がしやすくなります。
この操作により、分母から根号を取り除くことができました。分数計算では基本的なテクニックですね。
より複雑な式の場合も見てみましょう。
(2+√37)/√37 = (2+√37)/√37 × √37/√37 = (2√37+37)/37
計算精度についても考慮が必要です。近似値を使う場合、どの段階で丸めるかが結果に影響を与えます。
例えば、√37 × √37を計算する場合を考えてみましょう。
近似値での計算: 6.08 × 6.08 = 36.9664
近似値を使った場合、わずかな誤差が生じることがわかります。複雑な計算では、この誤差が蓄積される可能性があるため注意が必要ですね。
37の平方根が登場する実際の問題例
続いては、√37が実際に使われる場面を確認していきます。
幾何学の問題でよく登場するのが、三平方の定理を使った計算でしょう。
直角三角形で、2辺の長さが1と6のとき、斜辺の長さは?解答:
斜辺² = 1² + 6² = 1 + 36 = 37
したがって、斜辺 = √37 ≒ 6.08
座標平面上での距離の計算にも使われます。
点A(1, 2)と点B(2, 8)の距離は?解答:
距離² = (2-1)² + (8-2)² = 1² + 6² = 37
したがって、距離 = √37 ≒ 6.08
物理の問題でも√37は登場することがあります。ベクトルの大きさを求める際などに出てくるでしょう。
| 分野 | 使用場面 | 具体例 |
|---|---|---|
| 幾何学 | 三平方の定理 | 直角三角形の辺の長さ |
| 座標幾何 | 2点間の距離 | 平面・空間での距離計算 |
| 物理 | ベクトルの大きさ | 速度・力の合成 |
他の平方根との比較
最後に、√37を他の平方根と比較して理解を深めていきましょう。
近い値を持つ平方根を並べてみると、相対的な大きさがわかりやすくなります。
√37 ≒ 6.083
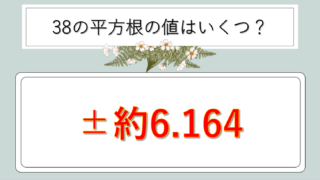
√38 ≒ 6.164
√39 ≒ 6.245
√40 ≒ 6.325
√37は√36とかなり近い値であることがわかるでしょう。一方、√40になると6.3を超え、かなり差が開いてきます。
素数の平方根をいくつか比較してみましょう。
| 素数 | 平方根の近似値 | 語呂合わせ例 |
|---|---|---|
| 2 | 1.414 | 一夜一夜に人見頃 |
| 3 | 1.732 | 人並みに奢れや |
| 5 | 2.236 | 富士山麓オウム鳴く |
| 37 | 6.083 | ろくまるはな |
√2、√3、√5は頻出するため、多くの人が覚えています
が、√37も覚えておくと計算がスムーズになる場面があるでしょう。
まとめ
以上、37の平方根について詳しく解説してきました。
√37 ≒ 6.08という値を覚えておき、必要に応じて計算方法を使い分けることで、様々な問題に対応できるはずです。
素数であるため簡単にできないという特徴も理解しておくと、他の平方根との違いがわかりやすくなるでしょう。数学の学習や実生活での計算に、ぜひ活用してみてください。