よく算数や数学において、図形中の線分の長さを計算する場面が多くでてきます。
特に、長方形などの図形ではさまざまな特徴があるため、着目されるケースが非常に多いです。
例えば、長方形の対角線の長さを求めるためには、どのように処理するといいのか理解していますか。
ここでは長方形の各辺の長さと対角線の長さの変換方法について解説していきます。
目次
長方形の長さの計算方法
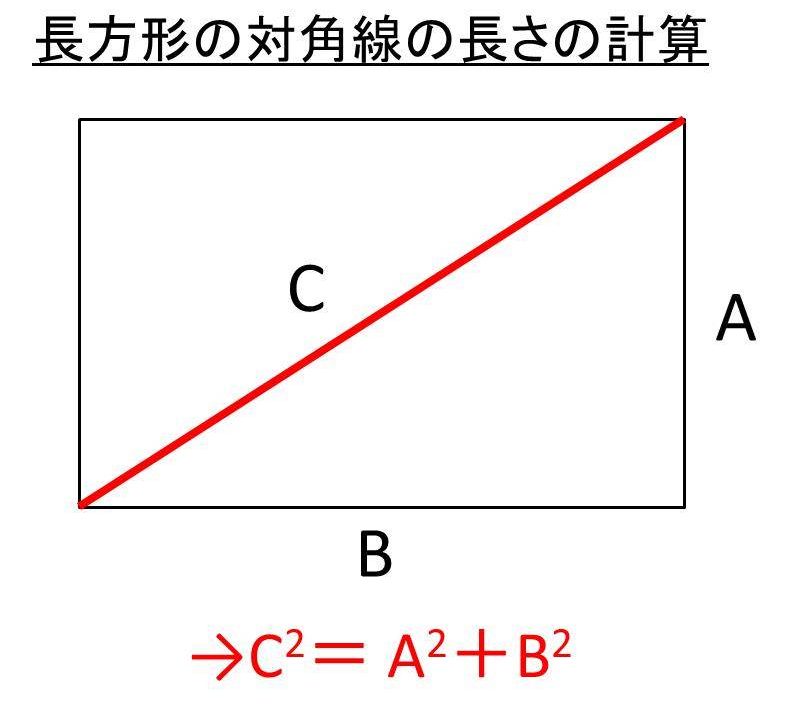
まず、長方形の対角線を図示すると以下の通りとなります。
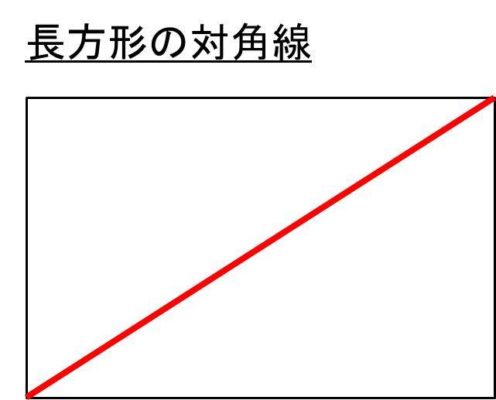
ここで長方形の対角線の長さを求めるためには、長方形の縦と横と対角線において、三平方の定理(A^2+B^2=C^2)を適用するといいです。なお、長方形は、正方形のときとは異なり、縦と横の長さが異なることに気を付けましょう。
例えば、長方形の縦の長さをA、横の長さをB、対角線の長さをCとすると、C2=A^2 + B2という式が成立します。
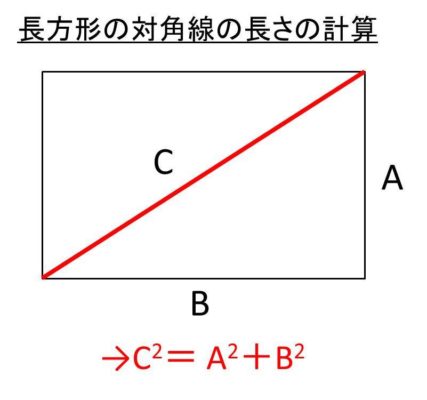
ここでの両辺のル-トをとることによって、√C^2=C=√(A^2 + B^2)と求めることができるわけです。

これが、長方形の対角線の長さを求める公式といえます。
長方形の対角線の長さを求める計算問題を解いてみよう
それでは、長方形における辺と対角線の長さの換算に慣れるためにも、実際の数値を用いて計算問題を解いてみましょう。
例題1
ある長方形の縦の長さは3cmであり、横の長さは4cmです。この長方形における対角線の長さはいくらになるでしょうか。
解答1
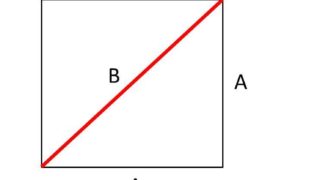
上の公式を適用します。なお、イメージしにくいときは以下のよう、図を書いてみるといいです。
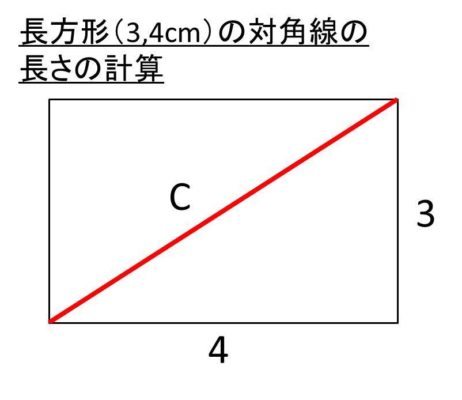
対角線の長さ=√(3^2 + 4^2)=5 と求めることができました。
続いて、もう一題長方形の対角線の長さの問題にチャレンジしていきましょう。
問題2
ある長方形いおける縦の長さは12cmであり、横の長さは5cmであるとします。この長方形における対角線の長さを計算していきましょう。
解答2
こちらも上の公式を元に計算していきましょう。こちらも形がよくわからないときは作図しましょう。

すると、対角線の長さ=√(12^2 + 5^2 ) =13と求めることができました。
きちんと理解しておきましょう。
まとめ
ここでは、長方形の辺の長さから対角線の長さに変換する方法について解説しました。
長方形における対角線の長さは、三平方の定理から求めることができ、対角線の長さ=√縦の長さ^2 + 横の長さ^2 で求めることができます。
後は、計算ミスに注意して長方形における対角線の長さを求めていきましょう。
長方形の対角線の計算に慣れ、より算数・数学を楽しんでいきましょう。