コサイン分の一、サイン分の一、タンジェント分の一など三角関数の逆数の積分は慣れていないと難しいですよね。
ここでは、「これら1/cosθ、1/sinθ、1/tanθの積分の解き方」について解説していきます。
目次
1/cos(コサイン分の一)の積分の計算方法
1/cosxの積分のやり方は決まっており、以下の流れで対応するといいです。
①1/cos=cosx/cos^2(x)という形に変形する

②続いて、cos^2(x)=1-sin^2(x)に変換する。
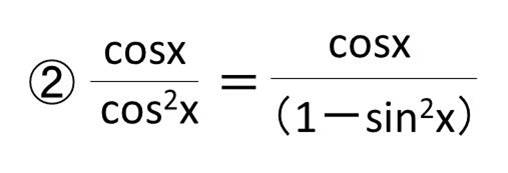
③1-sin^2(x)=(1+sinx)(1-sinx)と式変形する。
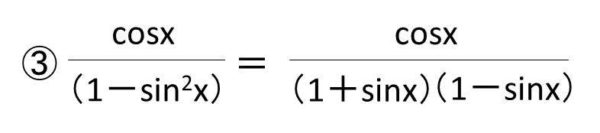
④項を分解する。
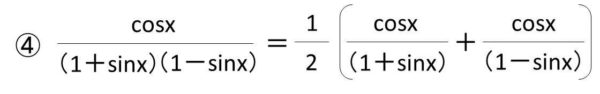
この分母にsinx、分子のcosxの形にしておくと、積分できるということを覚えておくといいです。詳しくは以下のlog(sinx)、log(cosx)の微分の仕方で解説しています。
※Logsinxの微分
⑤実際に積分を実行する
ここまで1/cosxの式変形が出来ましたら、この数式に対して積分していきます。

⑥log(1+sinx)の微分がcos/(1+sinx)であることを活用する
各々の項の積分を実行していきましょう。
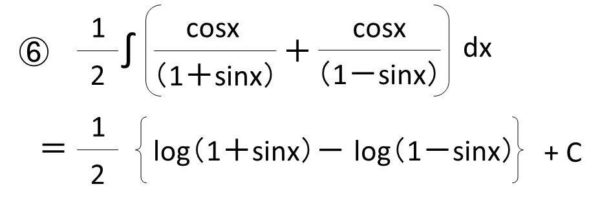
⑦式を簡略化する
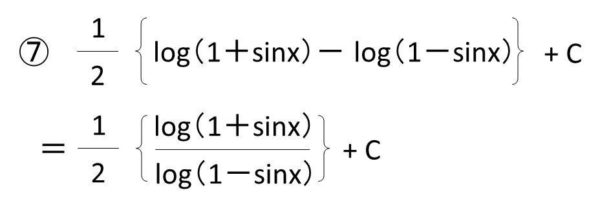
このようにして、1/cosx(コサイン分の一)の計算が実行されるのです。基本的にパターン問題と言えるため、きちんと慣れておきましょう。
1/cos(コサイン分の一)の積分の計算方法【三角関数の逆数】
同様に、1/sinxの積分も実行してみましょう。流れは1/cosの積分とほとんど同じです。以下で詳細の手順を確認していきます。
①1/sinx=sinx/sin^2(x)という形に変形する
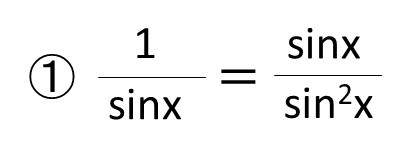
②続いて、sin^2(x)=1-cos^2(x)に変換する。
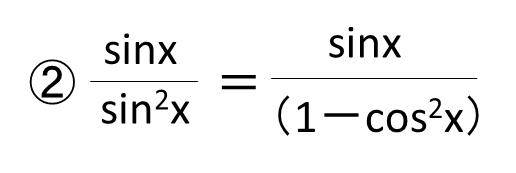
③1-cos^2(x)=(1+cosx)(1-cosx)と式変形する。
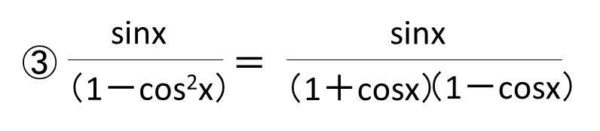
④項を分解する。
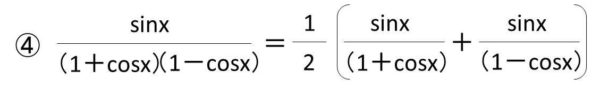
この分母にcosx、分子のsinxの形にしておくと、積分できるということを覚えておくといいです。詳しくは以下のlog(sinx)、log(cosx)の微分の仕方で解説しています。
※Logxの微分
⑤実際に積分を実行する
ここまで1/sinxの式変形が出来ましたら、この数式に対して積分していきます。
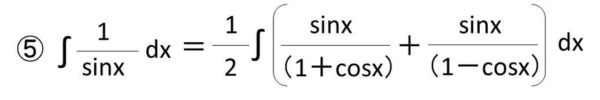
⑥log(1+sinx)の微分がcos/(1+sinx)であることを活用する
各々の項の積分を実行していきましょう。
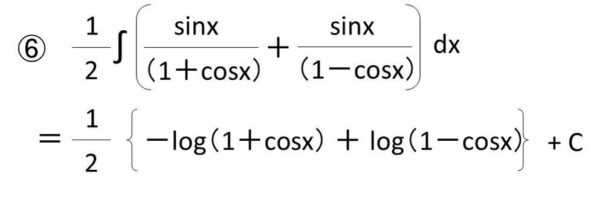
⑦式を簡略化する
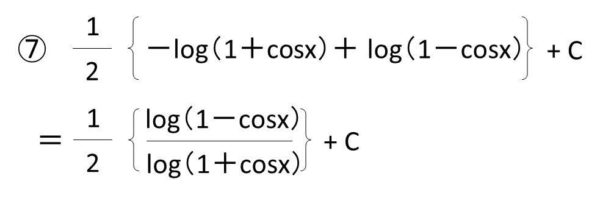
このようにして、1/sinx(サイン分の一)の計算が実行されるのです。1/cosの求め方と併せて理解しておきましょう。
1/tanx(タンジェント分の一)の積分のやり方【cot(コタンジェントの積分)】
最後にもう一つの三角関数の逆数の積分を実行していきます。
ここで、tanx=sinx/cosxと、分母と分子にsinとcosが来ている式であるため、積分は比較的容易に対応できます。
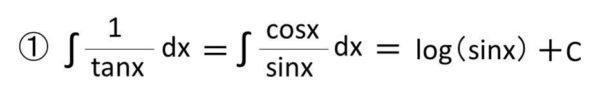
これでタンジェント分の一の積分は終了なのです。
きちんと理解しておきましょう。
まとめ
ここでは、1/cosx、1/sinx、1/tanxの積分の計算の仕方について解説しました。
1/cosや1/sinの積分では、まず分母に元の三角関数の2乗、分子に元の三角関数の形にして式変形してから、積分計算を実行するようにしましょう。なお、1/tanはそのまま積分を計算していくといいです。
さまざまな積分計算に慣れ、数学をより楽しんでいきましょう。