よく数字に関する問題として、その数は「Xの倍数なのかどうか」を判定するものが出題されます。
2の倍数や5の倍数であれば比較的容易に計算することができますが、3などの倍数は判断するのは難しいですよね。
ここでは、その数値が3の倍数かどうかを簡単に見分ける方法について解説していきます。
目次
3の倍数かどうかを判別する方法
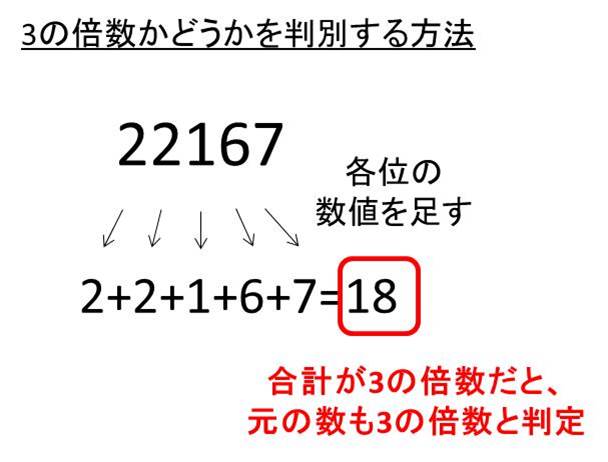
ある数字が3の倍数であるかどうかを簡単に判定するには、「各々の数値を足し合わせた合計が3の倍数かどうか」を考えればいいです。つまり、各々の位の数値の和が3で割りきれるのであれば、その数字は3の倍数と判別できるわけです。
たとえば、「22167」という桁数の大きな数字を考えたとします。パッと見は、この数字が3で割り切れるのかどうか判別しにくいですよね。
ここで上の方法を活用してみましょう。
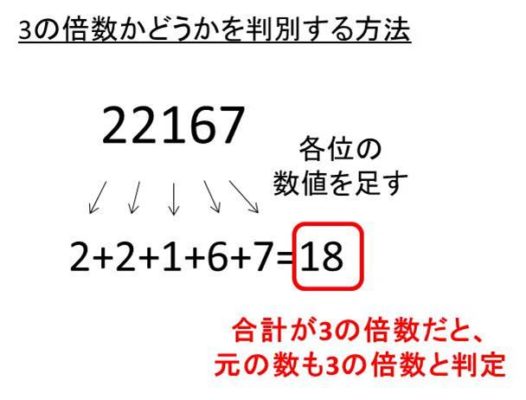
今回の場合では、2+2+1+6+7=18となり、各位の合計が3の倍数であることがわかります。つまり、この「22167」という数値は3の倍数であると判定できるわけです。
3の倍数の判定方法の証明
それでは、この3の倍数の判定方法はなぜ成立するのかということについて、証明していきます。
上述のような、ある5桁の数値があるとします。
このとき、各々の位の数値を1の位から順に、a,b,c,d,eとしていくと、以下のような数値となります。

すると、この数値はa+ 10b+ 100c+1000d+10000eと書けるわけです。
この計算式を整理していくと、a+(9b+b)+(99c+c)+(999d+d)+(9999e+e)=3(3b + 33c + 333d + 3333e) + (a+b+c+d+e)となります。

このとき、前の項は3の倍数であるため、各位の数値のみを足し合わせたものが3の倍数であれば、元の数も3の倍数であると見分けることができるわけです。
3の倍数かどうかの判定方法その2
ただ、この3の倍数を見分ける方法であっても桁数が大きくなると多少計算が複雑になります。
このようなケースでは、各位を足し合わせるときに少し工夫をするといいです。
よく数値の計算を簡単にするために、10や100などのまとまった数を作りながら計算する方法がありますよね。
2、8、1、9、5の足し算を行うときには、まず「2と8」「1と9」を足してから最後に5を足すようなものです。するとすぐに25と計算できるのです。
これを3の倍数の判定方法にも活用していきます。つまり、3の倍数となる組み合わせを作っていきながら計算すればいいのです。なお、3の倍数はそのままですでに3の倍数であるため、無視するといいです。
上述の22167という数値であれば、「最も左の2と中央の1で3」「左から2番目の2と最も右の7で9」、残りは6という3の倍数となり、合計値は3の倍数と簡単に判定できるわけです。
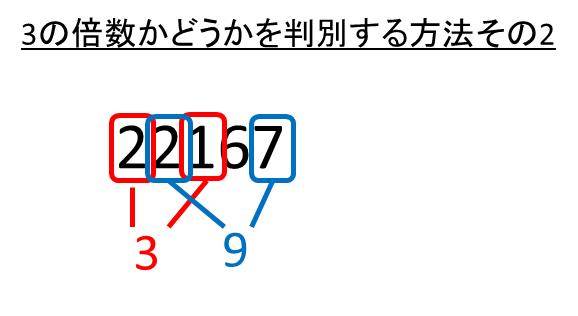
こちらの方が、より簡単に3の倍数かどうか判別できるためおすすめです。
あなたに適した3の倍数を見分ける方法を見つけ、数の扱いを楽しんでいきましょう。
まとめ
ここでは、3の倍数の判別方法とその証明の仕方について解説しました。
3の倍数かどうかを見分けるためには、各位の各々の数値を足し合わせたものが3の倍数となるかどうかを考えればいいです。
なお、計算を簡単にするためには、足し合わせるときに3の倍数を作りながら計していくようにしましょう。
さらに、証明方法は上述の通りですが、これも覚えておくと判別方法を忘れずに済むためきちんと理解しておきましょう。
3の倍数の判定方法などの数字の扱いに慣れることによって、より計算を楽しんでいきましょう。