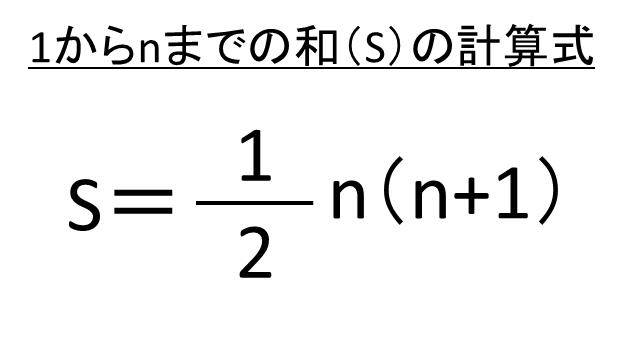科学的なデータを解析する際に、よく1からnまでの自然数の和を求めることが多くあります。
このような場面で、すべて普通に計算していたら非常に時間がかかってしまいます。そのため、簡単に計算する工夫が大事になります。
ここでは、この自然数の和の公式と計算方法について解説していきます。
目次
1からnまでの和の公式【自然数の和】
1からnまでの和を求める公式S（総和）＝1/2 n（n+1）となります。
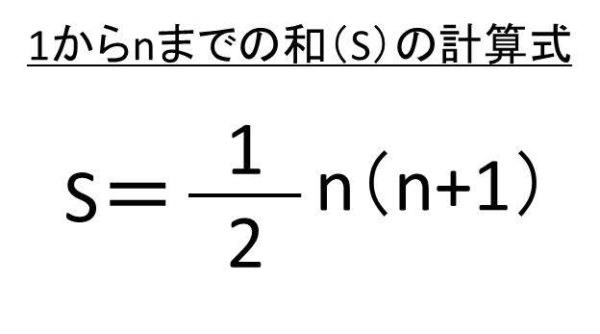この自然数の和の公式の導出方法は以下の通りです。
まず総和S＝1+2+ ・・・（n－1） + nという計算式が成り立ちます。なお、足し算であるため、足す順番を入れ替えても結果は同じであり、S＝n + (n-1) +・・・+ 2 + 1 と表すことができます。
ここで「元の順序の数式」と「逆に並び替えた数式」を足しあわせます。すると、以下のような状態となります。
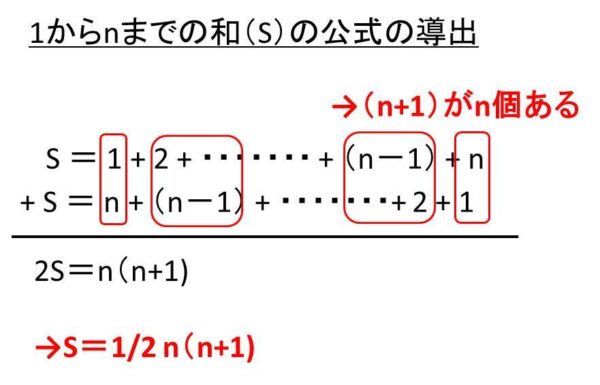
2S＝（n+1 ）+ （n－1 +2）+ ・・・（2+n-1）＋（1+n）＝n（n+1）という計算式が成立するわけです。
よって、S＝1/2 n(n+1)という1からnまでの整数を足し合わせた式が成立するのです。
この式を使用すれば桁数が大きな自然数の和も簡単に算出することができるため、特に上の証明方法をきちんと理解しておきましょう。
1からnまでの総和の計算問題を解いてみよう
それでは、連続した自然数の総和の計算に慣れるためにも、練習問題を解いていきましょう。
1から50までの自然数の総和を計算してみよう
まずは、50までの足し算を行ってみましょう。
公式：1/2 n(n+1)に従い、一括で総和を求めていきます。単純にnに50を代入すればいいだけであるため、S=1/2・50・51＝1275と計算されました。
1から100までの和を求めてみよう
続いて、1から100までの整数の総和を算出してみましょう。
こちらも上の式を利用して、S＝1/2 ・100 ・101＝5050が合計値となります。
1から200までの和の計算方法
さらに大きい数値である200までの足し合わせを行ってみます。
よって、S=1/2・200・201＝20100が数値の合計となります。
1から365までの和の出し方
今度は、1年365日にまつわる数字の「365」まで足していってみましょう。
上の計算式に従うと365までの自然数の合計値はS＝1/2 ・365・366＝66795と計算できるのです。
まとめ
ここで、1からnまでの数値の合計を求める方法について解説しました。
1からnまでの自然数の和を計算するときは、公式S＝1/2n(n+1)を利用するといいです。
このnまでの整数の合計を求める計算式は、1+2+・・・+nとそれを逆にした、n+n-1+・・・2+1を足し合わせ、(n+1)がn項あるものが2Sに相当することから導出できます。
なお、1から50までの和、1から100までの和など、結局は上の総和の公式を利用さえすれば対応できることを理解しておきましょう。
数学の楽しさを理解し、より毎日を楽しんでいきましょう。
