様々な事業を育てていく場合など、その成長曲線が指数関数的な成長をすることが基本です。
一方で、指数関数的成長とは逆の位置付けとしてある用語に対数関数的成長というものがあります。
この指数関数的成長と対数関数的成長はとのような意味があり、どう違いがあるのでしょうか。
ここでは、指数関数と対数関数の定義も踏まえて、これらの成長曲線の違いについて解説していきます。
目次
指数関数の定義とグラフ
一般的な指数関数とは、計算式y= a b^x で表される関数のことを指します(ここでbは1以外)。

例えば、a,bの係数を2,3とした指数関数を数値を計算すると以下の通りとなります。

この数値を横軸x、縦軸yのグラフ(指数関数のグラフ)にすると以下のようになります。
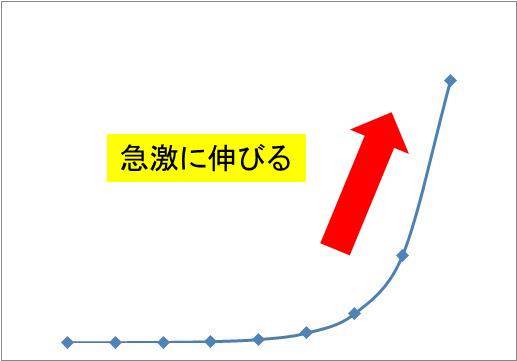
指数関数のグラフの特徴は、ある地点から急激に伸びることといえます。
そして、指数関数とセットで学ぶことが多い関数として、対数関数というものがあり、以下で確認していきます。
対数関数の定義とグラフ
対数関数とは、数式y=alogb(x)と表記される関数のことを指します。

係数a=2,b=3として対数の数値計算を行うと以下のようになります。
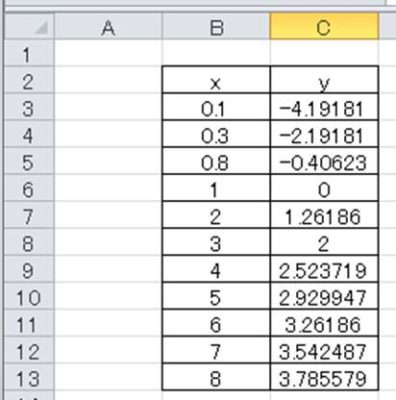
なお、この対数の数値を元にグラフ化すると以下の通りとなります。
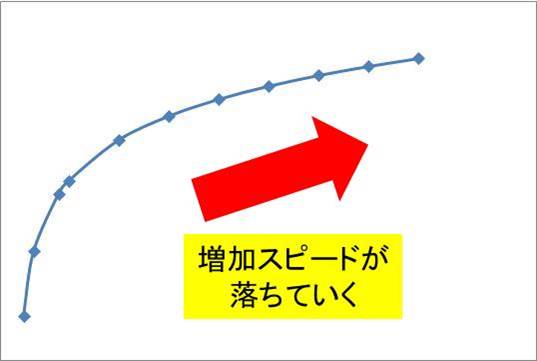
つまり、対数関数のグラフはxの数値が大きくなるにつれ、yの増加具合がなだらかになっていく曲線となるのです。
指数関数的成長と対数関数的成長の違い
このように指数関数と対数関数(指数と対数)には違いがあります。そして、これらの曲線を事業などの成長曲線(総資産などを数値化したもの)にあてはめて考えたときに、指数関数的成長と対数関数的成長という用語が出てくるのです。
つまり、指数関数的に一気に成長するような成長のことを指数関数的成長と呼び、逆に事業の伸びなどが失速する成長度合いのことを対数関数的成長とうわけです。
もちろん、事業主、経営者からすると、対数関数的な成長ではなく、指数関数的な成長の方が望ましく、それをみな目指しています。
こちらのブログでも指数関数的な成長をできるように頑張っていきます!
まとめ
ここでは、「指数関数や対数関数の定義」から「指数関数的成長や対数関数的成長の違い」まで解説しました。
指数関数とはy=ab^xという式で表現でき、一方で対数関数とはy=alogb(x)で表すことができるものです。
グラフにすると一目瞭然ですが、指数関数のグラフは急激に上昇していく一方で、対数関数のグラフは途中からyの数値の上昇が失速します。
そして、指数関数的な成長と対数関数的な成長とはこのグラフのことをなぞったものであり、成長曲線が片方は伸び、片方は失速することを表しています。
きちんと、指数関数的成長と対数関数的成長の違いを理解して、自分の事業を指数関数的成長に導いていきましょう。