数学の学習において、平方根の計算は避けて通れない重要なテーマです。
特に47のような素数に近い数の平方根は、日常生活ではあまり馴染みがないかもしれません。しかし、理系の試験や実務計算では頻繁に登場するため、しっかりと理解しておく必要があるでしょう。
√47は無理数であり、循環しない無限小数として表されます。そのため、正確な値を覚えるのではなく、近似値や計算方法を身につけることが実用的。
本記事では47の平方根について、その値から覚え方、計算テクニックまで徹底的に解説していきます。語呂合わせも紹介するので、暗記が苦手な方もぜひ参考にしてください。
それではまず、47の平方根の基本的な値について解説していきます。
目次
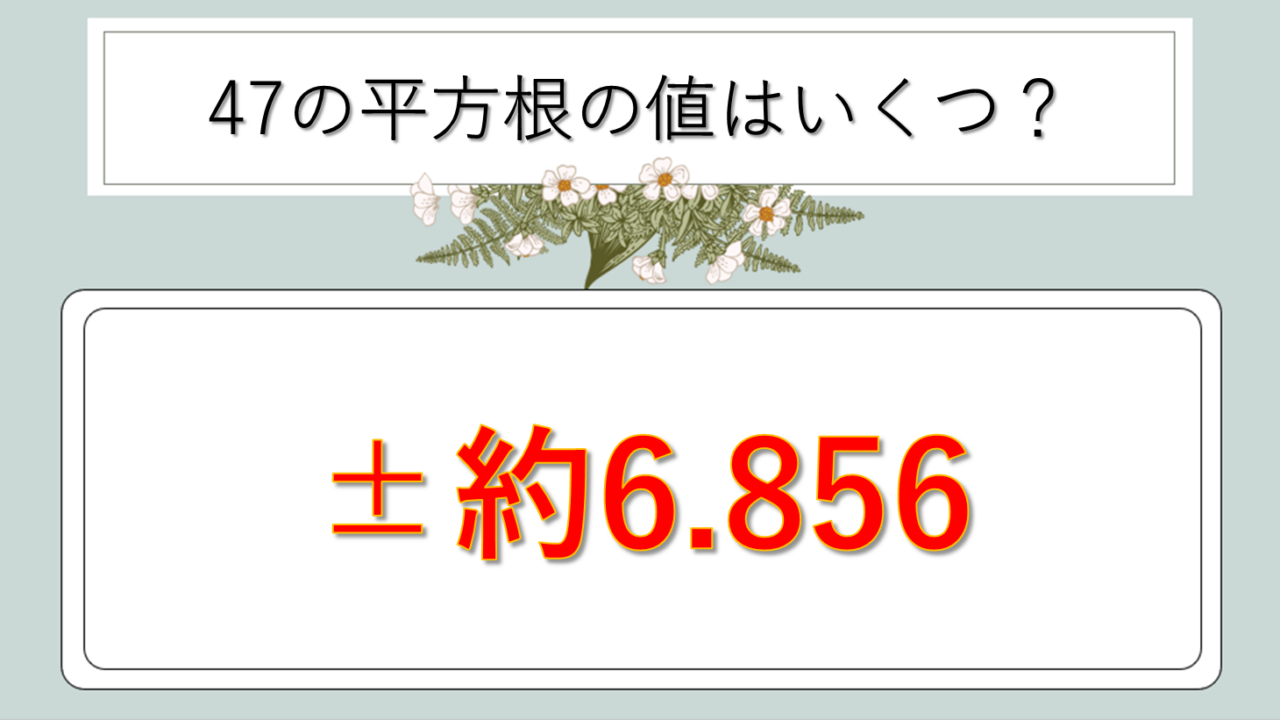
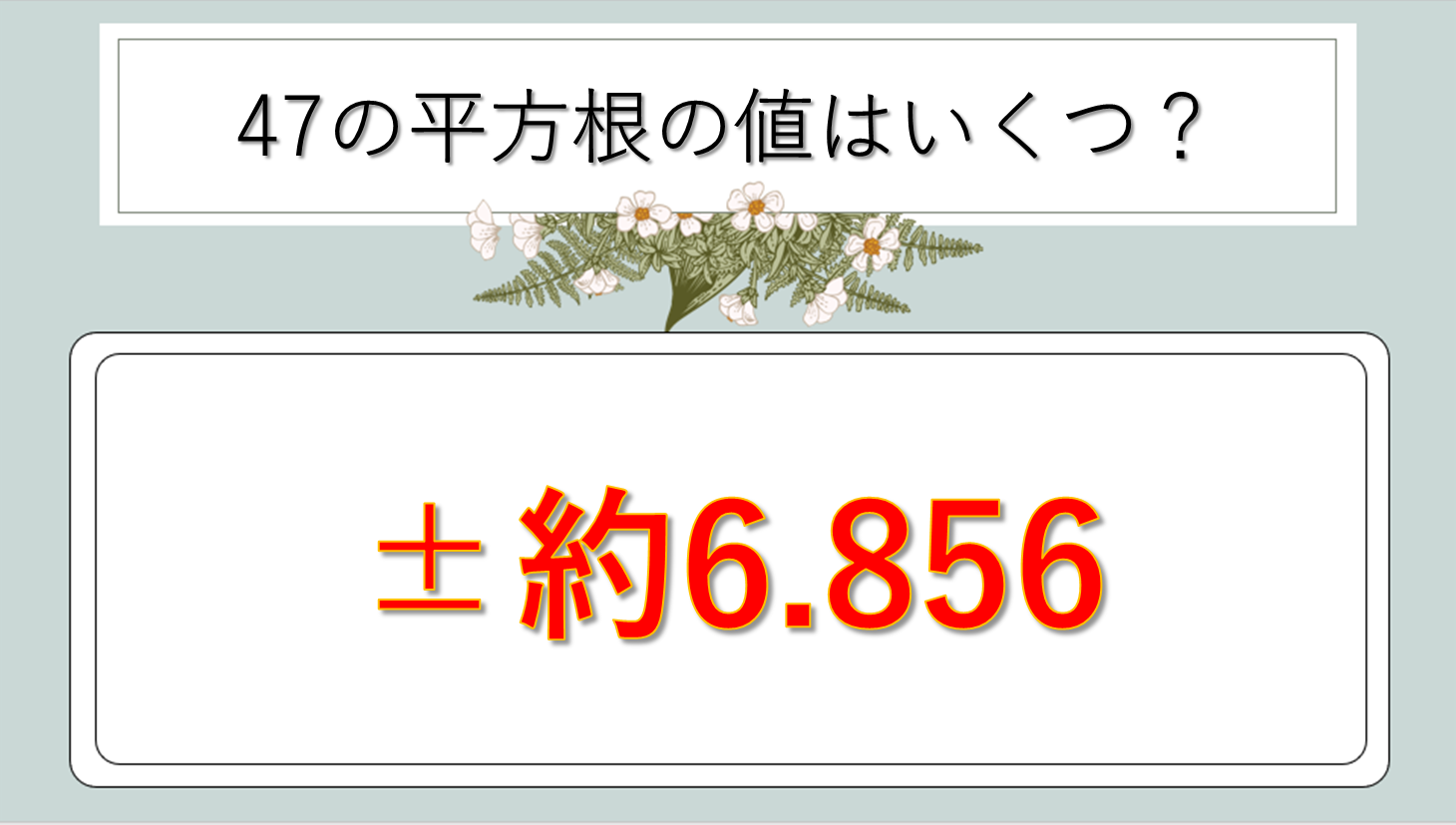
√47の値はいくつ?正確な近似値を知ろう
47の平方根の値を電卓やコンピュータで計算すると、以下のようになります。
√47 ≒ 6.85565460040104…
小数第5位まで表すと6.85565となり、実用的な計算では小数第2位までの6.86や、小数第3位までの6.856を使用することが多いでしょう。
では、この値がどの程度正確なのか確認してみましょう。
6.86²を計算すると
6.86 × 6.86 = 47.0596
誤差は約0.06で、かなり近い値ですね。
精度を上げて6.856で計算してみると、さらに正確な結果が得られます。
| 近似値 | 2乗した値 | 誤差 |
|---|---|---|
| 6.8 | 46.24 | -0.76 |
| 6.85 | 46.9225 | -0.0775 |
| 6.86 | 47.0596 | +0.0596 |
| 6.856 | 47.004736 | +0.004736 |
この表からわかるように、小数第3位まで覚えておけば十分な精度が確保できるわけです。試験や実務では、求められる精度に応じて使い分けることが重要でしょう。
続いては、47の平方根を簡単に理解するための覚え方を確認していきます。
√47の覚え方は?語呂合わせで楽々暗記
数学の学習において、語呂合わせは非常に有効な記憶術。√47についても、いくつかの語呂合わせを活用することで、スムーズに覚えられます。
最も一般的な語呂合わせは以下のとおりです。
「6.856」→「ロバ、ゴロゴロ」
「6.85」→「ロバ、ゴー」
6をロ(ろく)、8をバ(は)、5をゴ(ご)と読み替えることで、リズミカルに覚えられるでしょう。ロバがゴロゴロしている様子をイメージすれば、さらに記憶に定着しやすくなります。
他にも創造的な語呂合わせとして、次のようなものがあります。
6.856 → 「むっ、ハムゴロー」
6.85 → 「ロックバンド、ゴー」
6.9 → 「ろくな」(大まかな近似値として)
自分だけのオリジナル語呂合わせを作ってみるのもおすすめ。個人的な経験やイメージと結びつけることで、より強固な記憶として定着するからです。
ただし、語呂合わせはあくまで補助ツール。計算方法や概念をしっかり理解した上で活用することが、真の数学力向上につながるでしょう。
√47を簡単にする方法は?素因数分解で考える
平方根を簡単にするとは、ルートの中の数を素因数分解して、平方数を外に出すこと。例えば√12なら√(4×3)=2√3のように変形できます。
では、47の場合はどうでしょうか。
47は素数であるため、これ以上簡単にすることはできません。素因数分解しても47=47×1となり、平方数が含まれていないからです。
| 数 | 素因数分解 | 簡単にした平方根 |
|---|---|---|
| 12 | 2² × 3 | 2√3 |
| 48 | 2⁴ × 3 | 4√3 |
| 47 | 47 | √47(そのまま) |
| 75 | 3 × 5² | 5√3 |
このように、47は素数という特性上、√47という形が最も簡潔な表現となります。無理に変形しようとせず、そのまま扱うのが正解です。
ちなみに、47前後の数で簡単になるものを確認しておくと理解が深まるでしょう。
√45 = √(9×5) = 3√5
√48 = √(16×3) = 4√3
√49 = 7(完全平方数)
√50 = √(25×2) = 5√2
47の前後には簡単になる数が多く存在しているため、比較しながら学習すると効果的です。
√47の計算方法は?手計算でのアプローチ
電卓を使わずに√47を求める方法はいくつかあります。ここでは実用的な計算テクニックを紹介していきましょう。
まず基本となるのが、完全平方数との比較による推定法。47の前後にある完全平方数を確認してみます。
6² = 36
7² = 49
36 < 47 < 49より、6 < √47 < 7
この範囲がわかったら、さらに詳しく見ていきます。47は49に近いため、√47は7に近い値になるはず。
次に使えるのが、開平法(筆算による平方根の計算法)です。少し複雑ですが、原理を理解すれば電卓なしでも精度の高い計算が可能。
より実用的なのは、ニュートン法を簡略化したアプローチでしょう。
√47の近似値を求めるステップ
1. 初期値を6.8とする(6²=36、7²=49の中間やや上)
2. 47÷6.8≒6.912
3. (6.8+6.912)÷2≒6.856
4. これが√47の良い近似値
このように、推測値と47をその値で割った商の平均を取ることで、精度の高い近似値が得られます。
もう一つの実用的な方法として、近い完全平方数からの補正計算があります。
√49 = 7を基準とする
47 = 49 – 2より
√47 ≒ 7 – 2/(2×7) = 7 – 2/14 ≒ 7 – 0.143 ≒ 6.857
この方法は微分の考え方を応用したもので、かなり正確な近似値が得られるでしょう。実際の値6.85565と比較しても、誤差はわずかです。
√47を使った応用問題と実生活での活用
平方根の理解は、単なる暗記ではなく実践的な応用力が重要。√47がどのような場面で使われるか見ていきましょう。
幾何学の問題では頻繁に登場します。例えば直角三角形の斜辺を求める際、ピタゴラスの定理を使用します。
例題:2辺が5と6の直角三角形の斜辺の長さは?
斜辺² = 5² + 6² = 25 + 36 = 61
斜辺 = √61 ≒ 7.81
同様に、ある直角三角形の斜辺が√47なら
2辺の組み合わせは複数考えられます
また、円の面積から半径を求める逆算でも平方根が活躍します。
| 状況 | 計算式 | √47の使用例 |
|---|---|---|
| 円の面積から半径 | r = √(S/π) | S=47πなら r=√47 |
| 正方形の面積から辺 | a = √S | S=47なら a=√47 |
| 速度計算 | v = √(2gh) | 2gh=47なら v=√47 |
物理学では、運動エネルギーや電気抵抗の計算でも平方根が必要になります。特に二次方程式の解を求める際には、判別式に平方根が含まれることが多いでしょう。
二次方程式 x² – 13x – 2 = 0 の解は
x = (13 ± √(169+8))/2 = (13 ± √177)/2
このように√の中が素数や大きな数になることは珍しくありません
統計学における標準偏差の計算でも、分散の平方根を求める必要があります。データ分析の現場では日常的に使用される計算です。
√47と他の平方根との比較で理解を深める
数の性質を理解するには、周辺の数との比較が効果的。√47を他の平方根と比べてみましょう。
まず、近い整数の平方根を並べてみます。
| 数 | 平方根 | 近似値 | 特徴 |
|---|---|---|---|
| 43 | √43 | 6.557 | 素数 |
| 45 | 3√5 | 6.708 | 簡単化可能 |
| 47 | √47 | 6.856 | 素数 |
| 49 | 7 | 7.000 | 完全平方数 |
| 50 | 5√2 | 7.071 | 簡単化可能 |
この表から、√47は7よりわずかに小さく、完全平方数に非常に近いことがわかります。そのため、7を基準に考えると計算しやすいでしょう。
また、よく使われる平方根と比較すると、大きさの感覚がつかめます。
√2 ≒ 1.414
√3 ≒ 1.732
√5 ≒ 2.236
√47 ≒ 6.856
√50 ≒ 7.071
√47は√50の約97%の大きさ。このような相対的な関係を把握しておくと、計算ミスに気づきやすくなります。
まとめ:√47をマスターするためのポイント
ここまで47の平方根について、さまざまな角度から解説してきました。重要なポイントを整理しておきましょう。
√47 ≒ 6.856(または6.86)
語呂合わせ:「ロバ、ゴロゴロ」
47は素数なので簡単化できない
6 < √47 < 7の範囲に存在
計算方法としては、完全平方数との比較や近似計算法を身につけることが実用的です。特に7²=49を基準として、わずかに小さい値と理解しておけば、暗算でもおおよその値が推定できるでしょう。
試験対策としては、小数第2位までの6.86を覚えておけば十分なケースがほとんど。より高い精度が必要な場合は6.856まで記憶しておくとよいでしょう。
実生活や学問の場面でも、幾何学的な計算や物理の公式、統計分析など、さまざまな応用があります。単なる数値の暗記ではなく、概念として理解することが大切です。
平方根の学習は、数学的思考力を養う絶好の機会。√47を通じて、推定力、計算力、そして数の感覚を磨いていってください。繰り返し練習することで、自然と身についていくはずです。