数学の世界には、さまざまな数の平方根が登場します。中でも42の平方根は、日常的な計算や数学の問題でしばしば出会う値の一つ。しかし、この値は無理数であるため、正確な値を小数で表すことはできません。
そこで今回は、42の平方根の値や覚え方、近似値の求め方について詳しく解説していきます。計算方法や語呂合わせも紹介しますので、受験勉強や日常の学習にぜひお役立てください。
それでは、まず42の平方根の基本的な値について解説していきます。
目次
42の平方根の値はいくつ?
42の平方根は、√42と表記されます。この値は無理数であり、循環しない無限小数として続いていくのが特徴です。
√42 ≒ 6.48074069840786…
正確な値を小数で書き表すことはできませんが、実用上は小数第2位や第3位までの近似値を使用することが多いでしょう。

√42を簡単にすると、42=2×3×7と素因数分解できますが、平方数の因数を含まないため、これ以上簡単な形には変形できません。
つまり、√42は最も簡単な形であり、そのまま√42として扱うのが一般的です。
42の平方根が無理数である理由
42は平方数(1、4、9、16、25…)ではないため、その平方根は有理数にはなりません。42を素因数分解すると2×3×7となり、同じ数の2乗の形を取り出せないことからも明らかです。
42の平方根の近似値と覚え方は?
続いては、42の平方根の近似値と実用的な覚え方を確認していきます。
小数第3位までの近似値
実際の計算では、以下のような近似値を使用することが多いでしょう。
| 桁数 | 近似値 |
|---|---|
| 小数第1位 | 6.5 |
| 小数第2位 | 6.48 |
| 小数第3位 | 6.481 |
| 小数第5位 | 6.48074 |
日常的な計算では、6.48程度の精度があれば十分なケースがほとんど。より精密な計算が必要な場合には、電卓や計算ソフトを使用するのが賢明です。
記憶に残る覚え方のコツ
√42の値を覚えるには、いくつかの方法があります。まず、6と7の平方数を思い出してみましょう。
6² = 36
7² = 49
42は36と49の間にあるため、√42は6と7の間の値になると推測できます。36よりも42の方が49に近いわけではなく、むしろ36に近いことから、√42は6.5よりも少し小さい値だと判断できるでしょう。
語呂合わせで楽しく覚えよう
数値の暗記には、語呂合わせが効果的です。続いては、√42の語呂合わせについて見ていきます。
おすすめの語呂合わせ
√42 ≒ 6.48という値を覚えるための語呂合わせをいくつかご紹介しましょう。
「ろくはよ(6.48)」
「むしろよっぱ(6.48)」
シンプルなものほど記憶に残りやすいもの。自分なりの語呂合わせを作ってみるのも、記憶の定着には効果的です。
また、42という数字自体が「死に(4.2)」や「良い夫婦(4.2→よいふうふ)」など、さまざまな連想を生む数字でもあります。こうした連想と組み合わせることで、より印象に残る覚え方ができるかもしれません。
42の平方根の計算方法は?
ここからは、実際に√42を計算する方法について確認していきます。
電卓を使った計算方法
最も簡単な方法は、電卓の平方根機能を使うこと。多くの電卓には「√」ボタンがあり、以下の手順で計算できます。
1. 「42」と入力
2. 「√」ボタンを押す
3. 結果:6.48074069…
スマートフォンの電卓アプリでも、横向きにすると科学電卓モードになり、同様の計算が可能です。
筆算による開平法
電卓がない場合、手計算で平方根を求める「開平法」という方法があります。これは江戸時代から伝わる伝統的な計算手法ですが、現代ではあまり使われません。
興味深い方法ではありますが、実用性を考えると電卓や次に紹介する近似法の方が効率的でしょう。
ニュートン法による近似計算
数値計算の世界では、ニュートン法(ニュートン・ラフソン法)という手法がよく使われます。これは、初期値から出発して徐々に真の値に近づいていく方法。
√42を求める場合、以下の式を繰り返し適用します。
x_{n+1} = (x_n + 42/x_n) ÷ 2
初期値 x_0 = 6 とすると
x_1 = (6 + 42/6) ÷ 2 = (6 + 7) ÷ 2 = 6.5
x_2 = (6.5 + 42/6.5) ÷ 2 ≒ 6.4807692…
x_3 = (6.4807692 + 42/6.4807692) ÷ 2 ≒ 6.4807407…
わずか数回の計算で、かなり正確な値に到達できることが分かります。
他の平方根との比較で理解を深める
√42の値をより深く理解するために、近い値を持つ他の平方根と比較してみましょう。
| 平方根 | 近似値 | 参考 |
|---|---|---|
| √40 | 6.325 | 2√10と同じ |
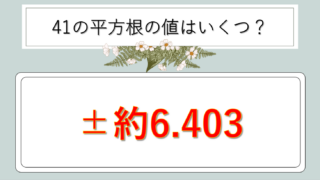
| √41 | 6.403 | 素数の平方根 |
| √42 | 6.481 | – |
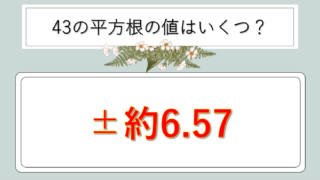
| √43 | 6.557 | 素数の平方根 |
| √44 | 6.633 | 2√11と同じ |
このように並べてみると、√42は6.4から6.5の間に位置することが視覚的に理解できるはず。隣接する平方根との差は約0.08程度であり、比較的等間隔に並んでいることも興味深い点です。
√42が登場する実際の場面とは?
数学の問題だけでなく、実生活でも√42が登場する場面があります。続いては、具体的な活用例を見ていきましょう。
三角形の辺の長さ計算
直角三角形の2辺がそれぞれ特定の長さの場合、斜辺の長さとして√42が現れることがあります。
例:直角三角形で、2辺の長さが1と√41の場合
または、√6と6の場合
斜辺 = √(1² + 41²) = √42(1つ目のケース)
斜辺 = √(6² + 6²) ≠ √42(このケースは異なります)
正確には、2辺が1と√41の場合、斜辺は√(1+41)=√42となります。
面積や体積の計算
正方形の面積が42の場合、1辺の長さは√42になります。このように、面積から辺の長さを逆算する場面で平方根が活躍するのです。
練習問題で理解を確認しよう
最後に、√42に関連する練習問題で理解を深めていきます。
基本問題
問題1:√42は6と7のどちらに近いか?
答え:6に近い(6²=36、7²=49で、42は36に近い)
問題2:√42 × √42 の値は?
答え:42(平方根の定義より)
問題3:2√42 の近似値は?
答え:2 × 6.481 ≒ 12.96
応用問題
実際の試験では、√42を含む計算問題が出題されることもあります。
問題:√168 を簡単にしなさい
解答:√168 = √(4×42) = 2√42
このように、√42自体は簡単にできませんが、他の平方根を簡単にする過程で√42が登場することがあるのです。
まとめ √42を完全マスター
ここまで、42の平方根について多角的に解説してきました。重要なポイントをもう一度確認しておきましょう。
√42 ≒ 6.48(小数第2位まで)
√42は無理数であり、これ以上簡単にはできない
6² = 36、7² = 49 から、6 < √42 < 7 と分かる
覚え方としては「ろくはよ(6.48)」という語呂合わせが使えます。計算方法は電卓が最も簡単ですが、ニュートン法などの近似計算法も理解しておくと応用が利くでしょう。
数学の学習では、このような基本的な平方根の値を感覚的に理解しておくことが大切。√42の値を覚えることで、関連する計算問題にもスムーズに対応できるようになるはずです。
日常の学習や試験対策に、ぜひこの知識を活用してください。