数学の学習を進めていると、平方根の計算に出会う機会は数多くあります。特に121という数字は、平方根を求める問題の中でも頻出する数値の一つでしょう。
この記事では、121の平方根の値について、基本的な計算方法から覚え方、さらには実用的な語呂合わせまで幅広く解説していきます。平方根の理解を深めることで、数学の応用力も大きく向上するはずです。
それでは早速、121の平方根の基本から確認していきましょう。
目次
121の平方根の値はいくつ?
それではまず、121の平方根の値について解説していきます。
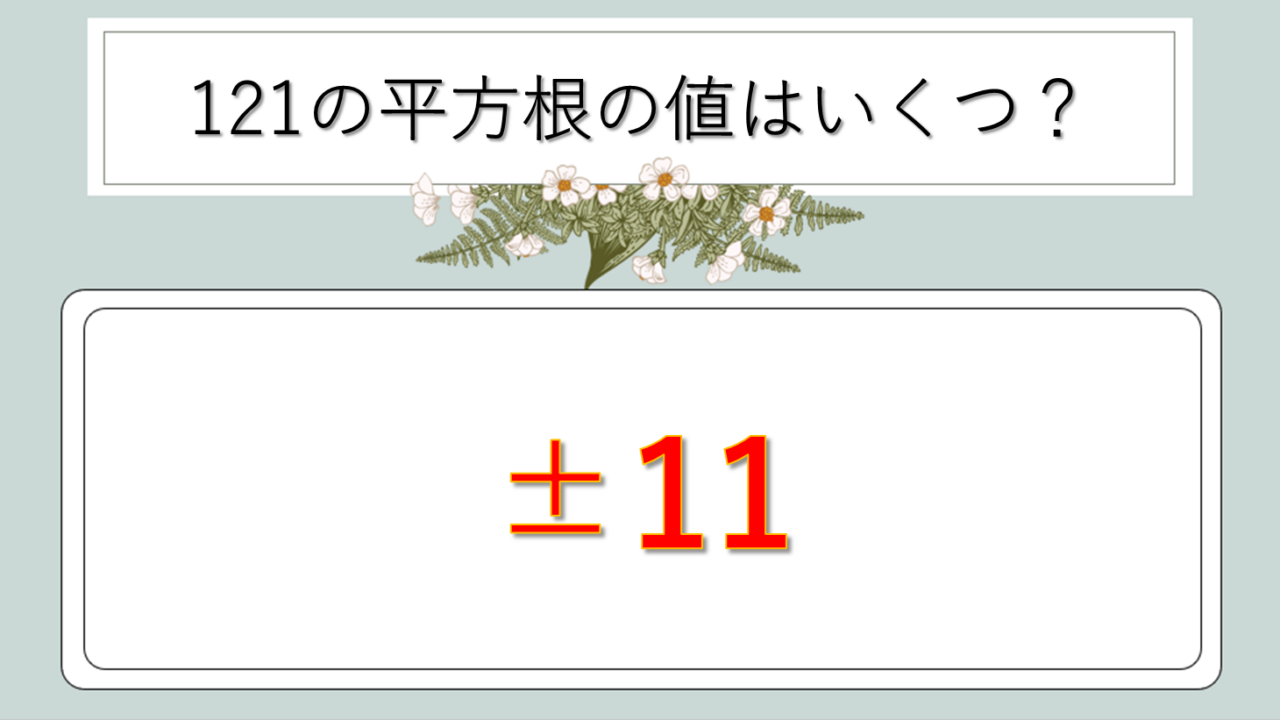
121の平方根は±11となります。つまり、√121 = 11、または-√121 = -11ですね。

なぜこのような値になるのでしょうか。平方根とは「2乗するとその数になる値」のことを指します。11×11=121、そして(-11)×(-11)=121となるため、121の平方根は±11となるわけです。
重要ポイント
√121 = 11(正の平方根)
121の平方根全体では±11となる
数学の問題では、√の記号を使う場合は正の平方根のみを指すことが一般的でしょう。したがって√121と書かれていれば、答えは11となります。
一方で「121の平方根を求めよ」という問題の場合は、±11の両方を答える必要があるケースもあるため注意が必要です。
計算例
11² = 11 × 11 = 121
(-11)² = (-11) × (-11) = 121
よって √121 = ±11
121は完全平方数であり、整数の平方根を持つ数として覚えやすい特徴があります。
121の平方根の覚え方や語呂合わせは?
続いては、121の平方根の覚え方について確認していきます。
121の平方根は11という整数なので、実は語呂合わせを使わなくても比較的覚えやすい数値でしょう。しかし、より確実に記憶するための方法をいくつか紹介します。
パターン認識で覚える方法
121という数字自体に注目してみると、「1-2-1」という対称的な並びになっていますね。この美しい数字の並びと、答えの11という「1が2つ並ぶ数」を関連付けると覚えやすいです。
「121→11が2回→11」というイメージでしょうか。
掛け算の九九から連想する方法
11×11の計算は、九九の延長として覚えている人も多いはず。「11×11=121」という掛け算を先に覚えておけば、自動的に√121=11も導き出せます。
覚え方の例
11×11=121(いちいち、いちにいち)
「いちいち掛けると、いちにいち」
語呂合わせの例
もし語呂合わせで覚えたい場合は、以下のようなフレーズも使えるでしょう。
「121(いいにい)は、11(いい)の二乗」
シンプルではありますが、数字の読み方をそのまま活用した覚え方です。
また、「いい兄(121)は、いい(11)」という覚え方も面白いかもしれません。自分なりの語呂合わせを作ってみるのも記憶定着には効果的ですね。
121の平方根の計算方法は?
続いては、121の平方根の計算方法を確認していきます。
平方根を求める方法には、いくつかのアプローチがあります。ここでは代表的な計算方法を紹介しましょう。
素因数分解を使う方法
121を素因数分解すると、より平方根が求めやすくなります。
素因数分解の手順
121 = 11 × 11 = 11²
√121 = √(11²) = 11
この方法では、121が11の2乗であることが明確になるため、平方根が11であることが一目瞭然でしょう。
試行錯誤で求める方法
どの整数を2乗すると121になるかを探す方法もあります。
10² = 100(小さすぎる)
11² = 121(ちょうど良い)
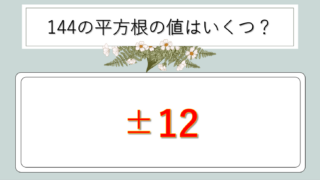
12² = 144(大きすぎる)
このように段階的に確認していけば、答えに辿り着けますね。
完全平方数の表から確認する方法
完全平方数を表にまとめておくと、すぐに確認できて便利です。
| 数値(n) | 平方(n²) | 平方根(√n²) |
|---|---|---|
| 9 | 81 | 9 |
| 10 | 100 | 10 |
| 11 | 121 | 11 |
| 12 | 144 | 12 |
| 13 | 169 | 13 |
表を見れば、121は11²であることがすぐに分かります。このような表を作成しておくと、他の平方根の問題にも素早く対応できるでしょう。
121の平方根を簡単にするとどうなる?
続いては、121の平方根を簡単にする方法について確認していきます。
121の平方根は既に11という整数なので、これ以上簡単にする必要はありません。つまり√121=11が最もシンプルな形です。
重要ポイント
√121 = 11(これが最も簡単な形)
根号の中に残す必要はない
一般的に、平方根を簡単にするというのは「根号の中をできるだけ小さくする」作業を指します。例えば√72なら√(36×2)=6√2のように変形できるでしょう。
しかし121の場合は完全平方数であるため、根号を完全に外すことができるわけですね。
比較例
√72 = √(36×2) = 6√2(簡単にした形)
√121 = 11(既に最も簡単な形)
つまり、121の平方根に関しては「簡単にする」という作業自体が不要ということになります。
121の平方根の近似値や小数表示は?
続いては、121の平方根の近似値について確認していきます。
実は121の平方根は正確に11という整数なので、近似値を求める必要はありません。小数表示をしても11.0となるだけです。
数値表現
√121 = 11
小数表記 11.0
近似値 11.00000…
ただし、平方根の概念を理解するために、121に近い数の平方根と比較してみましょう。
| 数値 | 平方根 | 小数表示(近似値) |
|---|---|---|
| 120 | √120 | 約10.954 |
| 121 | √121 | 11.000 |
| 122 | √122 | 約11.045 |
このように、121の前後の数の平方根は無理数(循環しない無限小数)となりますが、121だけはぴったり11という有理数になることが分かりますね。
これが完全平方数の特徴です。
121の平方根を使った計算例
続いては、実際に121の平方根を使った計算例を確認していきます。
平方根の知識は、様々な数学の問題で活用されます。いくつか実践的な例を見てみましょう。
式の簡略化
例題1
√121 + √49 を計算せよ
解答 √121 = 11、√49 = 7
よって 11 + 7 = 18
このように、平方根を先に計算してから足し算を行います。
方程式への応用
例題2
x² = 121 を解け
解答 両辺の平方根をとると
x = ±√121 = ±11
方程式を解く際にも、平方根の知識が不可欠となりますね。
面積から辺の長さを求める
例題3
面積が121cm²の正方形の一辺の長さは?
解答 一辺をxとすると x² = 121
x = √121 = 11cm
実生活の問題でも平方根は頻繁に使われます。図形の問題では特に重要でしょう。
連立的な計算
例題4
√121 × √9 ÷ √4 を計算せよ
解答 √121 = 11、√9 = 3、√4 = 2
よって 11 × 3 ÷ 2 = 33 ÷ 2 = 16.5
複数の平方根を含む計算でも、それぞれを整数に直してから計算すればスムーズに解けます。
121以外の覚えておきたい平方根
続いては、121以外にも覚えておくと便利な平方根を確認していきます。
数学の問題を効率的に解くためには、主要な完全平方数とその平方根を暗記しておくことが推奨されます。
| 完全平方数 | 平方根 | 計算式 |
|---|---|---|
| 1 | 1 | 1² |
| 4 | 2 | 2² |
| 9 | 3 | 3² |
| 16 | 4 | 4² |
| 25 | 5 | 5² |
| 36 | 6 | 6² |
| 49 | 7 | 7² |
| 64 | 8 | 8² |
| 81 | 9 | 9² |
| 100 | 10 | 10² |
| 121 | 11 | 11² |
| 144 | 12 | 12² |
| 169 | 13 | 13² |
| 196 | 14 | 14² |
| 225 | 15 | 15² |
これらの完全平方数を覚えておくと、計算のスピードが格段に上がります。特に1から15までの二乗の値は必須と言えるでしょう。
覚え方のコツ
完全平方数を覚える際は、規則性に注目すると良いです。
例えば、連続する完全平方数の差は奇数になるという性質があります。
完全平方数の差の規則
4 – 1 = 3
9 – 4 = 5
16 – 9 = 7
25 – 16 = 9
36 – 25 = 11
このように、差が3、5、7、9、11…と連続する奇数になっていますね。
平方根を学ぶ意義と応用
続いては、平方根を学ぶ意義について確認していきます。
平方根は単なる計算技術ではなく、様々な分野で実用的に使われる重要な概念です。
日常生活での応用
建築やインテリアでは、正方形の面積から一辺の長さを求める際に平方根を使います。例えば、121平方メートルの土地を正方形にするなら、一辺は11メートルになりますね。
理科での応用
物理では、速度や加速度の計算で平方根が頻繁に登場します。また、統計学では標準偏差の計算にも使われるでしょう。
上級数学への橋渡し
平方根は以下の分野の基礎となる
二次方程式の解の公式
三平方の定理
複素数の計算
平方根の理解は、これらの高度な数学概念を学ぶ上で不可欠です。
まとめ 121の平方根は11
121の平方根について、様々な角度から解説してきました。
√121 = 11という基本を押さえつつ、素因数分解や試行錯誤など複数の計算方法を理解しておくことが大切です。
121は「1-2-1」という対称的な数字であり、その平方根11も「1-1」と覚えやすい形をしています。このようなパターン認識を活用すれば、より確実に記憶できるでしょう。
また、121だけでなく他の完全平方数も合わせて覚えることで、数学の問題を素早く解く力が身につきます。平方根は日常生活から高度な数学まで幅広く応用される重要な概念ですので、しっかりマスターしていきましょう。