数学の問題を解いているとき、平方根の計算に出会うことは多いもの。特に196という数字は、日常生活や学習の中で頻繁に登場する値です。√196と聞いて、すぐに答えが浮かぶでしょうか。
平方根は中学数学で学ぶ重要な概念であり、高校数学や実生活でも応用される場面が多々あります。196の平方根を理解することで、平方根の性質や計算方法への理解が深まるはず。
本記事では、196の平方根の値や計算方法、覚え方のコツまで、わかりやすく解説していきます。語呂合わせや簡単な求め方も紹介するので、数学が苦手な方でも安心して読み進めていただけるでしょう。
それではまず、196の平方根の基本的な値について解説していきます。
目次
196の平方根の値はいくつ?【正確な答え】
196の平方根を求める前に、平方根とは何かを確認しておきましょう。平方根とは、2乗するとその数になる値のこと。つまり√196は、2乗すると196になる数を意味します。
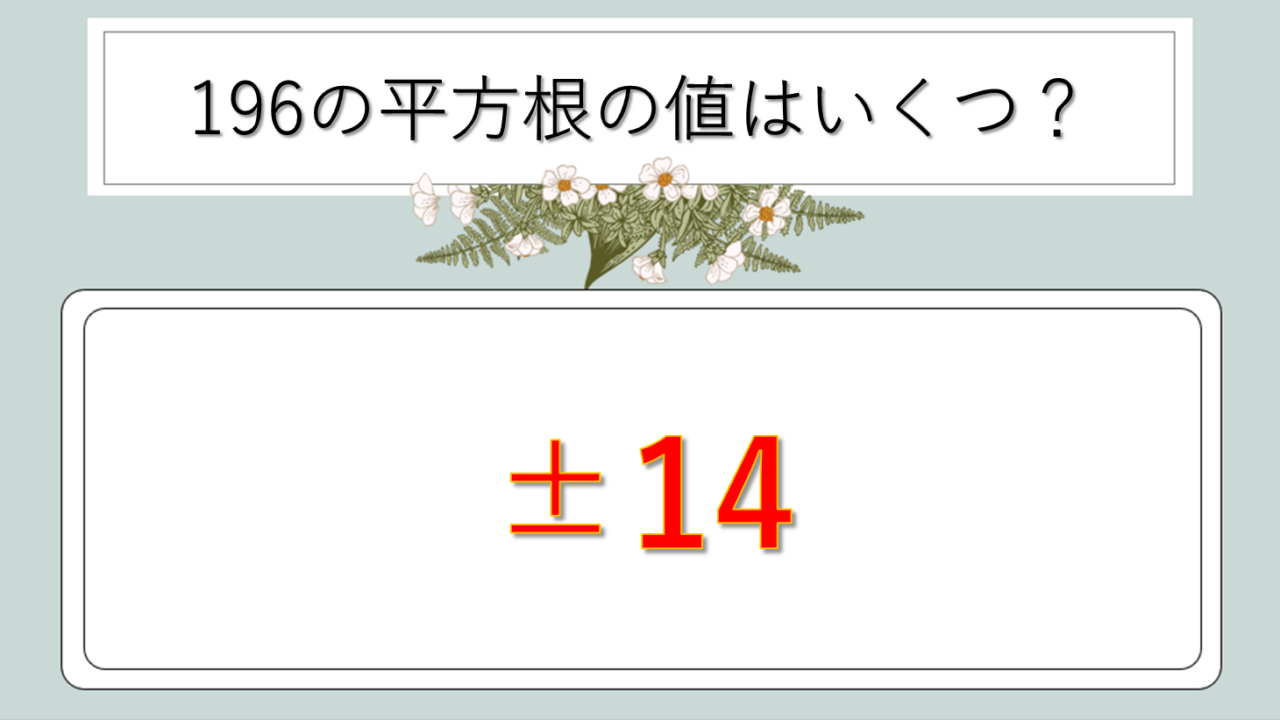
√196 = 14
結論から言えば、196の平方根は14です。これは正確な値であり、近似値ではありません。

なぜ14なのか。その理由は単純明快で、14×14=196だから。検算してみると確かに正しいことがわかるでしょう。
検算:14 × 14 = 196
したがって、√196 = 14
196は完全平方数と呼ばれる特別な数です。完全平方数とは、ある整数を2乗して得られる数のこと。√2や√3のように無理数になるケースとは異なり、196の平方根はきれいな整数になるのが特徴。
平方根には正と負の2つの値が存在することも覚えておきましょう。厳密には±14が答えとなりますが、一般的に√の記号は正の平方根を表すため、√196=14と表記します。
196の平方根の計算方法は?【素因数分解で求める】
続いては、196の平方根を実際に計算する方法を確認していきます。
最も確実な方法は素因数分解を利用する方法です。素因数分解とは、ある数を素数の積で表す手法のこと。
196を素因数分解すると:
196 = 2 × 98
196 = 2 × 2 × 49
196 = 2 × 2 × 7 × 7
196 = 2² × 7²
素因数分解ができたら、次は平方根の性質を使います。√(a²)=aという性質を利用すれば、計算は簡単。
√196 = √(2² × 7²)
√196 = √(2²) × √(7²)
√196 = 2 × 7
√196 = 14
この方法なら、どんな完全平方数でも確実に平方根を求められるでしょう。素因数分解は一見面倒に思えますが、正確性が高く、理論的にも納得できる方法です。
簡単に√196を求める方法は?【パターン認識】
素因数分解以外にも、もっと直感的な方法があります。それは完全平方数のパターンを覚えておく方法。
日常的によく使う完全平方数を以下の表にまとめました。
| 数値 | 2乗の値 | 平方根 |
|---|---|---|
| 10 | 100 | √100 = 10 |
| 11 | 121 | √121 = 11 |
| 12 | 144 | √144 = 12 |
| 13 | 169 | √169 = 13 |
| 14 | 196 | √196 = 14 |
| 15 | 225 | √225 = 15 |
| 16 | 256 | √256 = 16 |
10から20までの2乗を覚えておけば、多くの問題に対応できます。特に100、144、169、196、225あたりは試験でも頻出。
196が14の2乗だと知っていれば、計算せずとも瞬時に答えが出せるでしょう。これは数学的な理解というより、パターン認識による暗記法と言えます。
196の平方根の覚え方は?【語呂合わせテクニック】
数字を覚えるのが苦手な人には、語呂合わせが効果的です。196と14を結びつける語呂合わせをいくつか紹介しましょう。
「イクロー(196)は イシ(14)のように固い」
「イクロー(196)を イヨー(14)で割る」
「イクロー(196)、イッシー(14)」
語呂合わせは人によって覚えやすさが異なるもの。自分なりのオリジナル語呂合わせを作ってみるのも良いでしょう。
別の覚え方として、14×14という掛け算そのものを覚える方法もあります。九九の延長として、10台の掛け算を暗記しておくと便利。
11 × 11 = 121
12 × 12 = 144
13 × 13 = 169
14 × 14 = 196
15 × 15 = 225
こうしたパターンを頭に入れておけば、平方根の問題に素早く対応できるはず。繰り返し書いて練習することで、自然と身につきます。
196の平方根に近似値は必要?【正確な整数値】
続いては、196の平方根に近似値が必要かどうかを確認していきます。
結論から言うと、196の平方根は正確に14なので、近似値を考える必要はありません。√2≒1.414や√3≒1.732のように小数で近似する必要がないのです。
近似値が必要になるのは、√5や√7のような無理数の場合。これらは小数点以下が無限に続くため、実用上は適当な桁数で切り上げたり切り捨てたりします。
| 平方根 | 種類 | 値 |
|---|---|---|
| √4 | 有理数(整数) | 2(正確) |
| √5 | 無理数 | ≒2.236(近似) |
| √9 | 有理数(整数) | 3(正確) |
| √10 | 無理数 | ≒3.162(近似) |
| √196 | 有理数(整数) | 14(正確) |
196のような完全平方数は、計算が簡単で答えもきれい。これが完全平方数を学ぶメリットでもあるでしょう。
もし「√196≒14」と書いたら、厳密には正確ではありません。「≒」は「ほぼ等しい」という意味の記号なので、正確に等しい場合は「=」を使うべき。
√196を簡単にするとどうなる?【既に最簡形】
平方根の問題では「簡単にしなさい」という指示が出ることがあります。では、√196を簡単にするとどうなるのでしょうか。
√196を簡単にすると:14
√196は既に計算可能な形なので、そのまま14にするのが「簡単にする」ということ。ルートの記号を外して整数で表すのが最もシンプルな形です。
他の例も見てみましょう。
√50を簡単にする場合:
√50 = √(25×2) = √25 × √2 = 5√2
√196を簡単にする場合:
√196 = √(196) = 14
√50の場合は5√2という形に変形しますが、これ以上簡単にはできません。一方、√196は完全に整数化できるため、14が最終形態。
「簡単にする」とは、平方根の中身から完全平方数を括り出すこと。196は全体が完全平方数なので、括り出すと何も残らないわけです。
試験問題で「√196を簡単にせよ」と出たら、自信を持って14と答えましょう。これ以上簡単にはできないのだから。
196と関連する平方根の値は?【周辺の数字】
196の平方根を理解したところで、関連する数字の平方根も確認しておくと理解が深まります。
196の前後の完全平方数を見てみましょう。
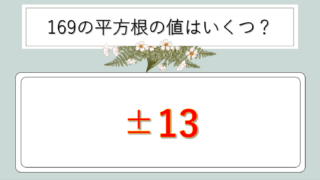
13² = 169 → √169 = 13
14² = 196 → √196 = 14
15² = 225 → √225 = 15
このように、完全平方数は規則的に並んでいることがわかります。169から196の差は27、196から225の差は29と、少しずつ広がっていくパターン。
196を分解した形の平方根も見てみましょう。
| 数値 | 分解 | 平方根 |
|---|---|---|
| 49 | 7² | √49 = 7 |
| 98 | 2×49 | √98 = 7√2 |
| 196 | 4×49 = 2²×7² | √196 = 14 |
196は49の4倍。49の平方根が7なので、196の平方根は7×2=14になるという関係性も見えてきます。
こうした数字の関連性を理解しておくと、暗算や概算の際に役立つでしょう。数学的な感覚が養われ、計算ミスも減らせるはず。
196の平方根を使った応用問題は?【実践例】
最後に、196の平方根を使った応用問題を確認していきます。
平方根は図形問題でよく登場します。例えば、面積が196平方センチメートルの正方形があったとしましょう。この正方形の一辺の長さは何センチでしょうか。
正方形の面積 = 一辺 × 一辺 = 一辺²
一辺² = 196
一辺 = √196 = 14センチメートル
このように、面積から辺の長さを逆算する際に平方根を使うのです。
別の例として、ピタゴラスの定理を使った問題も考えてみましょう。直角三角形で、2辺の長さがそれぞれ一定の値の時、斜辺を求める問題。
直角を挟む2辺が それぞれ 14センチメートルの直角三角形
斜辺² = 14² + 14² = 196 + 196 = 392
斜辺 = √392 = √(196×2) = 14√2 センチメートル
逆に、斜辺が14センチメートルで、一辺が何センチメートルか求める問題もあるでしょう。
数学だけでなく、物理や工学の分野でも平方根は頻繁に使われます。速度、加速度、エネルギーなどの計算で、2乗や平方根が登場するシーンは多いもの。
196の平方根が14だとすぐにわかれば、計算のスピードと正確性が向上します。基礎的な知識ほど、応用の場面で威力を発揮するのです。
まとめ 196の平方根は14【完全平方数として重要】
本記事では、196の平方根について詳しく解説してきました。
√196 = 14(正確な整数値)
196は14の2乗であり、完全平方数の代表例。素因数分解すると2²×7²となり、平方根は2×7=14と求められます。
覚え方としては、10台の2乗パターンを暗記する方法や、語呂合わせを使う方法が効果的でしょう。14×14=196という掛け算を繰り返し練習することで、自然と身につくはず。
近似値は不要で、正確に14という整数値が答え。「簡単にする」という指示があれば、ルートを外して14にするのが正解です。
平方根の理解は、図形問題や応用問題を解く上で欠かせません。196の平方根が瞬時にわかれば、計算時間の短縮につながり、試験でも有利になるでしょう。
数学の基礎を固めることで、より高度な問題にも対応できるようになります。196という数字を見たら、自信を持って「14だ」と答えられるようになってください。