数学の学習において、平方根は避けて通れない重要な概念です。
特に144の平方根は、完全平方数として基礎的な計算でよく登場するもの。受験や資格試験でも頻出の数値であり、正確に理解しておくことで計算速度が飛躍的に向上するでしょう。
本記事では144の平方根の値や計算方法を詳しく解説していきます。語呂合わせを使った覚え方や近似値の求め方、さらには実践的な応用例まで網羅的に紹介。
この記事を読めば、144の平方根に関する疑問がすっきり解消されるはずです。
それでは早速、144の平方根の基本的な値から確認していきましょう。
目次
144の平方根の値はいくつ?
それではまず、144の平方根の具体的な値について解説していきます。
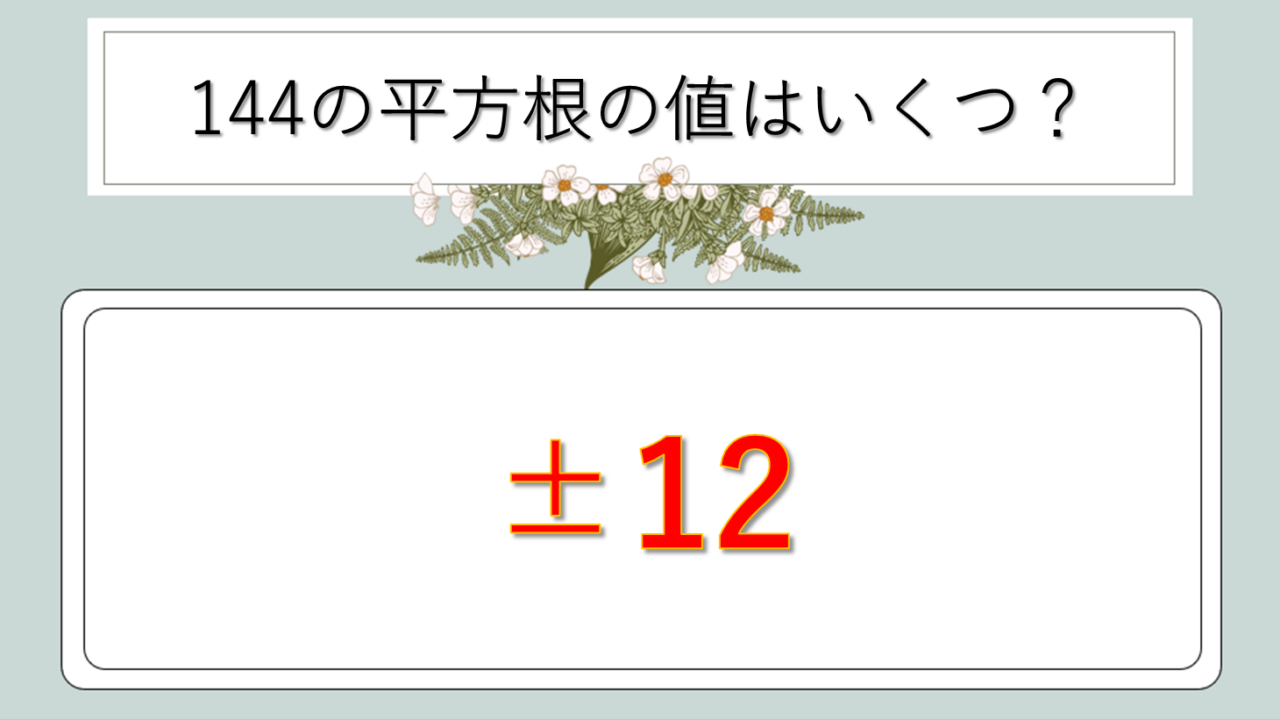
144の平方根、すなわち√144の値は12または-12となります。これは「2乗すると144になる数」を意味しており、12×12=144、(-12)×(-12)=144という関係から導かれるもの。
√144 = ±12
正の平方根:12
負の平方根:-12
一般的に√の記号を使う場合、正の平方根のみを指すことが多いです。そのため√144と書かれていれば12を、-√144と書かれていれば-12を答えることになるでしょう。

数学の問題で「平方根を求めよ」と指示された場合は、正負両方の解を答える必要があります。一方で「√144を求めよ」という問いには12のみを答えれば良いのです。
【例題】
x² = 144のときxの値を求めよ
【解答】
x = ±12
この区別をしっかり理解しておくことで、テストでの失点を防げるはず。平方根の概念は中学数学の重要な基礎となりますから、144のような基本的な数値で確実に定着させておきましょう。
144が完全平方数である理由
続いては、144が完全平方数である理由を確認していきます。
完全平方数とは、整数の2乗で表される自然数のこと。1、4、9、16、25、36…と続き、144もその仲間に含まれます。
| 整数n | n²(完全平方数) | √n² |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 4 | 2 |
| 3 | 9 | 3 |
| 4 | 16 | 4 |
| 5 | 25 | 5 |
| 10 | 100 | 10 |
| 11 | 121 | 11 |
| 12 | 144 | 12 |
144は12の2乗として表現できるため、完全平方数に分類されるわけです。完全平方数の平方根は必ず整数になるという特徴があり、計算が非常にシンプル。
素因数分解で考えると、144の構造がより明確になります。
144 = 2⁴ × 3²
= (2² × 3)²
= 12²
このように素因数分解すると、すべての素因数の指数が偶数になっていることが分かるでしょう。これが完全平方数の条件なのです。指数がすべて偶数であれば、ルートを外したときに整数になるという法則があります。
144以外にも、身近な完全平方数を覚えておくと計算がスムーズ。特に1から20までの2乗の値は暗記しておくことをお勧めします。
144の平方根の計算方法
続いては、144の平方根を実際に計算する方法を確認していきます。
最も基本的な方法は素因数分解を利用するアプローチです。先ほど示したように、144を素因数に分解すれば平方根が簡単に求められるでしょう。
【素因数分解による計算】
144 = 2 × 2 × 2 × 2 × 3 × 3
= 2⁴ × 3²
√144 = √(2⁴ × 3²)
= 2² × 3
= 4 × 3
= 12
素因数分解では、同じ数が2個ずつペアになっている部分をルートの外に出せます。2が4個あるので2個ずつのペアが2組、3が2個で1組のペアができ、それぞれ外に出すと2×2×3=12という計算に。
別の方法として、因数の組み合わせを試すやり方もあります。144を2つの同じ数の積で表せるかを考えるのです。
1×144、2×72、3×48…と試していくと、12×12=144という組み合わせを発見できるはず。この方法は小さな数であれば有効ですが、大きな数には向きません。
電卓を使わずに暗算で確認したい場合は、10の位と1の位に分けて考えるテクニックも便利。12²=(10+2)²=100+2×10×2+4=144という展開式を使えば、検算が可能です。
実務的には、よく使う完全平方数を暗記しておくのが最も効率的でしょう。
144の平方根の覚え方と語呂合わせ
続いては、144の平方根を記憶に定着させるための覚え方を確認していきます。
「144(いよいよ)12(十二支)」という語呂合わせが一般的。「いよいよ干支が一周する」というイメージで、144と12を結びつけられます。
144(いよいよ) → 12(十二支)
√144 = 12を連想
別の覚え方として、「1ダース×1ダース=1グロス」という商業単位を利用する方法もあるでしょう。1ダースは12個、12ダース(1グロス)は144個という関係性です。
日常生活と結びつけると記憶に残りやすいもの。例えば以下のような連想も有効。
・1年は12ヶ月、12年で144ヶ月
・12時間×12時間=144時間(6日間)
・12cm×12cm=144cm²
数学が苦手な人は、視覚的なイメージで覚えるのもお勧めです。12×12のマス目を描いて、全部で144個のマスがあることを確認する方法。実際に紙に描いてみると、平方の意味が体感的に理解できるはずです。
繰り返し計算問題を解くことで、自然と身につくパターンもあります。特に因数分解や平方根の計算では144が頻出するため、演習を重ねれば嫌でも覚えてしまうでしょう。
語呂合わせは記憶の補助ツール。最終的には144を見たら瞬時に12が浮かぶレベルまで習熟することが理想的です。
144の平方根の近似値について
続いては、144の平方根の近似値について確認していきます。
実は144の平方根は正確に12という整数値なので、近似値を求める必要がないというのが答え。完全平方数であるため、小数点以下は存在しません。
ただし、学習の観点から「もし144が完全平方数でなかったら」という仮定で近似値の求め方を理解しておくことは有意義でしょう。
| 数値 | 平方根の性質 | 値 |
|---|---|---|
| √143 | 完全平方数でない | 約11.958 |
| √144 | 完全平方数 | 12(正確) |
| √145 | 完全平方数でない | 約12.042 |
この表からわかるように、144の前後の数の平方根は無理数となり、小数点以下が続きます。しかし144だけはきれいに12という有理数になるのです。
平方根の近似値を求める一般的な方法として、ニュートン法や挟み撃ちの原理などがあります。例えば√143なら、12²=144だから12より少し小さい値と推測できるでしょう。
【挟み撃ちの例(√143の場合)】
11² = 121
12² = 144
121 < 143 < 144より
11 < √143 < 12
143は144に近いので、√143 ≒ 11.9~12.0
このような考え方を知っておけば、電卓がない状況でも大まかな平方根の値を推定できます。ただし繰り返しになりますが、√144については正確に12ですので近似の必要はありません。
144の平方根を簡単にする方法
続いては、144の平方根を簡単に表現する方法を確認していきます。
√144は最初から最も簡単な形である12に変形できます。これ以上簡単にする余地はありません。
一般的に平方根を簡単にするとは、ルートの中の数を最小にすることを指すもの。例えば√50なら5√2に、√72なら6√2に変形します。
【平方根を簡単にする一般的な手順】
1. ルートの中の数を素因数分解する
2. 同じ数が2個あるペアを見つける
3. ペアになった数をルートの外に出す
4. ルートの中に残った数を掛け算する
144の場合、この手順を適用すると以下のようになるでしょう。
√144 = √(2⁴ × 3²) = 2² × 3 × √1 = 4 × 3 = 12
ルートの中が1になったため、完全にルート記号を外せるわけです。√1=1なので省略できます。
逆に、144を含む複雑な平方根の計算では、この性質を活用することも。
√(144×2) = √144 × √2 = 12√2
√(144×3) = √144 × √3 = 12√3
√576 = √(144×4) = √144 × √4 = 12 × 2 = 24
144が含まれる式を見つけたら、144=12²という関係を使って簡略化を試みると良いでしょう。特に因数に144を持つ大きな数の平方根を計算する際に便利です。
平方根の計算は、いかに完全平方数を見抜けるかがポイント。144のような基本的な完全平方数を瞬時に判別できる力が、複雑な計算をスムーズにする鍵となります。
144の平方根の実践的な応用例
続いては、144の平方根が実際にどのような場面で使われるかを確認していきます。
幾何学において、正方形の面積と辺の長さの関係は最も基本的な応用例でしょう。面積が144cm²の正方形の1辺の長さは√144=12cmとなります。
正方形の面積 = 144cm²
1辺の長さ = √144 = 12cm
周の長さ = 12 × 4 = 48cm
ピタゴラスの定理を使う場面でも144は頻出。直角三角形の2辺が分かっているとき、残りの辺を求める計算で登場します。
【例】直角三角形の2辺が9cmと15cmのとき、斜辺の長さは?
斜辺² = 9² + 15²
= 81 + 225
= 306
斜辺 = √306(これは簡単にならない)
【別の例】2辺が5cmと13cmのとき、斜辺の長さは?
斜辺² = 5² + 13² = 25 + 169 = 194(これも簡単にならない)
統計学では、標準偏差や分散の計算で平方根が使われます。サンプルサイズが144のデータセットなら、√144=12という値が各種計算で現れることも。
物理学における速度や加速度の計算、工学における構造設計など、平方根は様々な分野で必要とされる概念です。144の平方根のような基本的な値を即座に答えられることは、これらの応用計算をスムーズに進める基礎力となるでしょう。
まとめ 144の平方根は12
144の平方根について、値や計算方法、覚え方まで詳しく解説してきました。
√144=12という関係は、数学の基礎中の基礎として確実に押さえておきたいポイント。完全平方数であるため計算が簡単で、様々な応用問題の土台となります。
語呂合わせ「いよいよ十二支」や「1ダース×1ダース=1グロス」といった記憶法を活用すれば、無理なく定着させられるはず。素因数分解を使った計算手順を理解しておけば、他の平方根の問題にも応用できるでしょう。
144の平方根をマスターすることは、数学の実力向上への確実な一歩。日々の学習や演習を通じて、自然と身につけていってください。