数学の基礎として欠かせない平方根の計算。特に整数の平方根は、さまざまな場面で活用される重要な知識です。今回は49の平方根について、その値や計算方法、覚え方まで詳しく解説していきます。
平方根は一見難しそうに見えるかもしれませんが、実は規則性を理解すれば簡単に扱えるもの。特に49のような完全平方数の平方根は、整数で表されるため、計算も覚えるのも比較的容易なのです。
それでは早速、49の平方根の基本から応用まで見ていきましょう。
目次
49の平方根の値はいくつ?【正確な数値】
それではまず、49の平方根の値について解説していきます。
49の平方根は7または-7です。数式で表すと√49 = ±7となります。
なぜ2つの値があるのでしょうか。これは平方根の定義に関係しています。平方根とは「2乗するとその数になる値」のこと。7×7=49であり、同時に(-7)×(-7)=49でもあるため、49の平方根には正の値と負の値の両方が存在するのです。

ただし、一般的に√(ルート)の記号を使う場合は正の平方根のみを指すことが多くなっています。そのため√49=7と表記されることが一般的です。
【確認】
7² = 7 × 7 = 49
(-7)² = (-7) × (-7) = 49
したがって、√49 = 7(主平方根)
49は完全平方数と呼ばれる特別な数です。完全平方数とは、整数の2乗で表される数のこと。1、4、9、16、25、36、49、64、81、100などがこれに該当します。完全平方数の平方根は必ず整数になるという特徴があるため、計算が非常にシンプルになるわけですね。
49の平方根の覚え方と語呂合わせ【記憶術】
続いては、49の平方根の覚え方を確認していきます。
49の平方根は7という整数なので、他の無理数の平方根と比べて覚えやすいのが特徴です。とはいえ、確実に記憶に定着させるためのテクニックをいくつか紹介しましょう。
掛け算の九九との関連付けが最も効果的な方法です。7×7=49は九九の延長として多くの人が自然に覚えている計算ですよね。この知識をそのまま平方根に応用すれば、√49=7も自動的に導き出せます。
語呂合わせで覚えるなら、以下のような方法もあるでしょう。
【語呂合わせの例】
「49(しく)→7(なな)」
「49(四苦)から7(ラッキー)へ」
「49日目に7つの悟り」
また、視覚的なイメージを使う方法も効果的です。49個の正方形を7×7の形に並べると、一辺が7個の正方形ができあがります。この図形的なイメージを頭に描くことで、平方根の概念そのものを理解しながら覚えられるのです。
さらに、完全平方数の一覧表を作成して眺めるのもおすすめ。1²=1、2²=4、3²=9…と続けていくと、7²=49が自然に目に入ってきます。
49の平方根の計算方法【簡単にする手順】
次に、49の平方根をどのように計算するのか、その方法を見ていきましょう。
素因数分解を使った方法
49の平方根を求める最も基本的な方法は素因数分解を利用することです。
【計算手順】
1. 49を素因数分解する
49 = 7 × 7 = 7²
2. 平方根を取る
√49 = √(7²) = 7
この方法は、より複雑な数の平方根を求める際にも応用できる重要なテクニックです。例えば√144であれば、144=12²なので√144=12と即座に導けます。
逐次近似法(ニュートン法)
もし49が完全平方数だと知らなかった場合、逐次近似法を使って答えに近づくこともできます。
この方法では、まず適当な値(例えば6)を予想し、以下の式を繰り返し適用していきます。
【ニュートン法の公式】
次の予想値 = (現在の予想値 + 49 ÷ 現在の予想値) ÷ 2
初期値を6とすると:
(6 + 49÷6) ÷ 2 = (6 + 8.167) ÷ 2 ≒ 7.083
(7.083 + 49÷7.083) ÷ 2 ≒ 7.001
(7.001 + 49÷7.001) ÷ 2 ≒ 7.000
このように、わずか数回の計算で正確な値7に収束していくのです。
49の平方根の近似値と小数表示【詳細な数値】
続いては、49の平方根の近似値について確認していきます。
49の平方根はちょうど7なので、実は近似値を考える必要はありません。小数で表しても7.000…と続くだけです。
| 表記方法 | 値 |
|---|---|
| 整数 | 7 |
| 小数第1位まで | 7.0 |
| 小数第5位まで | 7.00000 |
| 分数 | 7/1 |
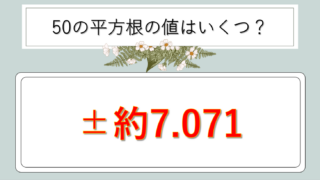
これは49が完全平方数であることの大きな利点です。一方、完全平方数でない数、例えば√50の場合は約7.071と無理数になり、正確に小数で表すことができません。
完全平方数の平方根は有理数(分数で表せる数)であり、それ以外の正の整数の平方根は無理数(分数で表せない数)になります。
参考までに、49の前後の数の平方根を比較してみましょう。
| 数 | 平方根 | 近似値 |
|---|---|---|
| 48 | √48 | 約6.928 |
| 49 | √49 | 7(正確) |
| 50 | √50 | 約7.071 |
このように、49だけが整数の平方根を持つことが明確に分かりますね。
49の平方根の応用と実用例【日常での活用】
最後に、49の平方根が実際にどのような場面で使われるのか見ていきましょう。
図形の計算での活用
平方根は図形の計算で頻繁に登場します。例えば、面積が49㎡の正方形があったとき、その一辺の長さは√49=7mとなるわけです。
【例題】
面積が49c㎡の正方形の一辺の長さは?
【解答】
正方形の面積 = 一辺 × 一辺
49 = 一辺²
一辺 = √49 = 7cm
同様に、直角三角形の辺の長さを求めるピタゴラスの定理でも平方根が使われます。
統計学での利用
統計学において、標準偏差や分散を計算する際に平方根は欠かせません。例えば、データのばらつきを示す分散が49だった場合、標準偏差は√49=7となります。
物理学での応用
物理の計算でも平方根は頻出です。例えば、自由落下の時間と距離の関係式などで使われます。落下距離が49mだった場合の計算などで、√49=7が登場するのです。
日常生活での活用
日常生活でも、正方形の土地や部屋の広さから一辺を求めたり、タイルの配置を考えたりする際に平方根の知識が役立ちます。49枚のタイルを正方形に並べるなら、7×7の配置が最適だと瞬時に判断できるでしょう。
【実用例】
・49枚の写真を正方形に配置 → 7×7
・49人のクラスを正方形の座席配置 → 7×7
・49㎡の庭の一辺 → 7m
まとめ:49の平方根をマスターしよう
49の平方根について、さまざまな角度から解説してきました。
重要なポイントを整理すると、49の平方根は±7であり、特に正の平方根として√49=7が使われることが多いということ。49は7²という完全平方数なので、平方根も整数になる特別な数なのです。
覚え方としては、7×7=49という掛け算との関連付けが最も効果的でしょう。素因数分解の方法を使えば、計算過程も明確に理解できます。
平方根の知識は数学の基礎であり、図形、統計、物理など幅広い分野で活用されています。49の平方根のような基本的な値をしっかり押さえることが、より高度な数学を学ぶ土台となるのです。
この機会に49の平方根だけでなく、他の完全平方数の平方根も合わせて覚えてみてはいかがでしょうか。1から100までの完全平方数とその平方根を一覧にしておくと、計算のスピードが格段に上がりますよ。
数学は積み重ねの学問です。基本をしっかりマスターして、次のステップへ進んでいきましょう。