数学の授業や日常の計算で、平方根に出会う機会は意外と多いもの。中でも√39という数値は、完全平方数ではないため、その値を暫定的に求めるのに少し工夫が必要となります。
√39の値はいくらなのか、どうやって計算すればいいのか、そして覚えやすい語呂合わせはあるのか。このような疑問を持つ方は少なくないでしょう。
本記事では、√39の正確な近似値から、実用的な計算方法、さらには記憶に残りやすい語呂合わせまで、包括的に解説していきます。平方根の理解を深めたい学生の方はもちろん、数学の面白さを再発見したい方にも役立つ内容です。
それではまず、√39の基本的な値について解説していきます。
目次
√39の値はいくつ?近似値を確認
√39の値を電卓で計算すると、約6.244997998…という数値が得られます。これは無限に続く無理数であり、完全には表現できない数値です。
実用的な場面では、小数第2位または第3位までの近似値で十分なケースがほとんど。そのため、一般的には以下のような近似値が使われています。
√39 ≒ 6.24(小数第2位まで)
√39 ≒ 6.245(小数第3位まで)
√39 ≒ 6.2450(小数第4位まで)
日常的な計算においては、√39 ≒ 6.24と覚えておけば十分でしょう。この値は、6と7の間に位置しており、6²=36、7²=49であることから、直感的にも理解しやすい範囲です。

より正確な値が必要な場合は、6.245という値を使用するのがおすすめ。科学技術計算などの精密な場面では、さらに桁数を増やした値が用いられることもあります。
√39の計算方法を詳しく解説
続いては、√39を実際に計算する方法を確認していきます。電卓を使わずに手計算で近似値を求める技法は、数学的思考を養う上でも有益です。
完全平方数からの推定法
最も基本的なアプローチは、√39に近い完全平方数を利用する方法。36と49という完全平方数に注目してみましょう。
6² = 36
7² = 49
36 < 39 < 49より、6 < √39 < 7
39は36と49のちょうど中間よりも36に近い位置にあります。具体的には、36から39までの差は3、36から49までの差は13。この比率から大まかな推定が可能です。
6 + 3/13 ≒ 6 + 0.23 = 6.23という計算により、おおよその値が求められるでしょう。
開平法による計算
より精密な値を求めたい場合は、開平法という伝統的な計算手法が活用できます。これは筆算で平方根を求める方法であり、以下のような手順で進めていきます。
まず39.00000000…のように小数点以下にゼロを付け、2桁ずつ区切ります。次に、最も近い完全平方数である36(6²)を利用して計算を開始。
6を仮の商として立て、36を引くと3が残ります。この3に続く00を降ろして300とし、これを124(6×2×10+4)で割ると、次の桁が2となる計算です。
この過程を繰り返すことで、6.244…という値が順次得られていきます。
ニュートン法による近似
数値計算の分野でよく用いられるのがニュートン法。この手法では、初期値を設定して反復計算を行います。
初期値をx₀ = 6とする
x₁ = (x₀ + 39/x₀)/2 = (6 + 6.5)/2 = 6.25
x₂ = (6.25 + 39/6.25)/2 ≒ 6.245
わずか2回の反復で、かなり正確な近似値に到達できるのが特徴です。このように、数学的な技法を駆使することで、電卓なしでも√39の値を求められます。
√39の覚え方と語呂合わせ
平方根の値を暗記する際、語呂合わせは非常に効果的なツール。√39についても、覚えやすいフレーズを用意しておくと便利でしょう。
「ロニー死後(6.24ご)」
6.24という数値を「ロニー死後」と読み替える語呂合わせ
また、別のバリエーションとして以下のような語呂合わせも考案できます。
「むつ(6)に死(2)後(4)」
「ロクに死後(6.24後)の世界」
「6人が2つに4つ(6.2.4)」
語呂合わせは個人の記憶スタイルに合わせて自由に作成可能。自分なりのストーリーを考えることで、より記憶に定着しやすくなります。
√39 ≒ 6.24という基本値さえ覚えておけば、テストや実務での計算にも対応できるはず。語呂合わせを活用して、楽しみながら学習を進めてみてください。
他の平方根との比較表
√39の値をより深く理解するため、周辺の数値と比較してみましょう。以下の表は、30台から40台の平方根をまとめたものです。
| 数値 | 平方根 | 近似値(小数第2位) |
|---|---|---|
| 36 | √36 = 6 | 6.00 |
| 37 | √37 | 6.08 |
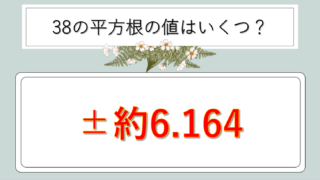
| 38 | √38 | 6.16 |
| 39 | √39 | 6.24 |
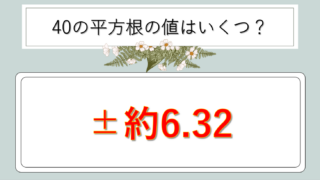
| 40 | √40 | 6.32 |
| 41 | √41 | 6.40 |
| 42 | √42 | 6.48 |
この表から分かるように、数値が1増えるごとに平方根は約0.08ずつ増加しています。ただし、この増加幅は一定ではなく、数値が大きくなるにつれて徐々に小さくなっていく傾向があります。
36は完全平方数(6²)であるため、√36は整数値となる点も注目すべきポイント。39はこの完全平方数から3だけ離れた位置にあり、その平方根も6からわずかに離れた値となっています。
√39を簡単にする方法はある?
平方根を簡単にする、つまり根号の中を簡略化するには、因数分解が鍵となります。では、√39は簡単にできるのでしょうか。
39を素因数分解してみましょう。
39 = 3 × 13
この結果を見ると、39は3と13という素数の積で表されます。どちらも平方数ではないため、√39はこれ以上簡単にすることができません。
もし39が、例えば√36や√100のように完全平方数であれば、整数として表現できたはず。また、√72 = √(36×2) = 6√2のように、平方数を因数として含んでいれば部分的に簡略化が可能です。
しかし39の場合、そのような因数が存在しないため、√39という形のまま扱うのが最も簡潔な表現となります。
√39は既に最も簡単な形
素因数分解しても平方数が含まれないため、これ以上の簡略化は不可能
計算上は6.24という近似値を使用し、数式上では√39のままで記述するのが一般的です。
√39の実用例と応用
√39という値は、実際にどのような場面で使われるのでしょうか。具体的な応用例を見ていきます。
幾何学での活用
正方形の対角線の長さを求める際、平方根の計算が必要になります。例えば、一辺の長さの二乗が39となるような長方形を考えてみましょう。
ある長方形の縦が3、横が√30の場合、対角線の長さは√(9+30) = √39となる計算です。このように、図形の寸法計算において平方根は頻繁に登場します。
物理計算での利用
物理学において、速度や加速度の計算でも平方根が用いられます。例えば、39メートル落下した物体の速度を求める際、v = √(2gh)という公式が使用可能。
重力加速度を約10m/s²とすると、v = √(2×10×39) = √780 ≒ 27.9m/sという計算になります。
統計学での標準偏差
データ分析において、標準偏差の計算にも平方根が欠かせません。分散が39である場合、標準偏差は√39 ≒ 6.24となります。
分散 = 39
標準偏差 = √39 ≒ 6.24
このように、√39は理論的な数学の枠を超えて、様々な実用場面で活躍している数値なのです。
√39に関する豆知識
最後に、√39にまつわる興味深い数学的性質をいくつか紹介していきましょう。
連分数表現
√39は連分数という形式で表現することも可能です。
√39 = 6 + 1/(4 + 1/(12 + 1/(4 + 1/(12 + …))))
この表現では、4と12が交互に繰り返されるパターンが現れます。連分数表現は、平方根の近似値を求める際にも利用可能な数学的手法です。
黄金比との関係
39という数自体は、数論において興味深い性質を持っています。3と13の積であり、どちらも重要な素数。特に13は、フィボナッチ数列にも登場する特別な数値です。
また、√39は約6.245という値であり、これは黄金比(約1.618)の約3.86倍に相当します。自然界の美しい比率と数学的に関連している点も興味深いでしょう。
計算の簡便性
実務的な観点では、√39を6.25と近似することも可能。この値は1/4の倍数であり、分数計算において扱いやすい利点があります。
√39 ≒ 6.25 = 25/4という近似は、厳密性を少し犠牲にする代わりに計算の簡便性を向上させる手法です。
精度と計算の容易さのバランスを考え、状況に応じて適切な近似値を選択することが重要となります。
まとめ
√39の値は約6.24であり、これは無理数として無限に続く小数です。完全平方数からの推定、開平法、ニュートン法など、様々な計算手法によって近似値を求められます。
語呂合わせ「ロニー死後(6.24ご)」を活用すれば、記憶にも定着しやすいでしょう。39は3×13と素因数分解されるため、√39はこれ以上簡単にできない最も基本的な形です。
幾何学、物理学、統計学など、多様な分野で√39の計算が必要となる場面があります。基本的な値さえ覚えておけば、実用的な計算にも十分対応可能。
平方根の理解を深めることは、数学的思考力を養う上でも非常に有意義です。√39という一つの数値を通じて、数学の奥深さと実用性を感じていただければ幸いです。