普段何気なく使用する言葉として、「速さ」や「速度」などの用語がありますよね。
これらは両方とも「速い」の名詞形のような言葉でありとても似ていますが、厳密には違いがあります。あなたはこれらの相違点についてきちんと理解していますか。
ここでは、速さと速度の違いや使い分けについて解説していきます。
目次
速さと速度の違い
速さも速度も、「移動距離÷かかった時間」によって、表すことができる物理量の一つです。
ただ、速度には大きさと向きがある量であるのに対して、速さとは大きさのみの量といえます。

つまり、速度の絶対値が速さになるともいえるわけです。
なお物理的な言葉を使用して速さと速度の違いについて考えますと、速さはスカラー量であるのに対し、速度はベクトル量といえます。
速度では軸と向きを記載する必要あり
なお、速度を記載する場合はx軸、y軸といった軸を設定する必要があります。これは上述のよう、速度には大きさだけではなく、向きも指定する必要があるためです。
例えば、以下のようx軸において右向きを正の方向と決めた場合、1時間あたりに右に5km/hで移動するのであれば、速度は+5km/hとかけるわけです。
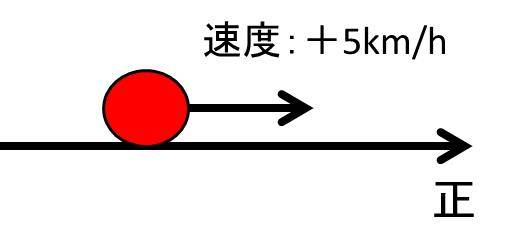
ちなみにこのときの速さは5km/hとなり、方向性は書かなくていいので、その数値と単位のみを書き、符号は省略するのが基本です。
逆に、真逆の方向に時速3km/hで移動するのであれば、速度:-3㎞/hといった具合で表現するわけです。
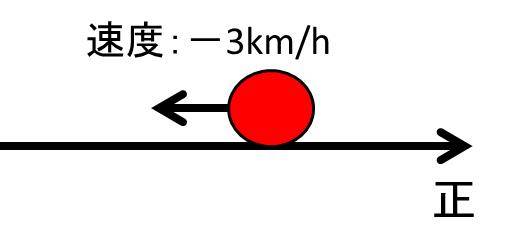
なお、このときの速さとしては、符号を除去した3km/hと換算できるのです。
速さと速度の違いを理解するための問題
それでは、速さや速度などのスピードに関する用語の扱いに慣れるためにも、練習問題を解いていきましょう。
例題1
ある自動車が道路Aにおいて、時速80㎞で移動しています。今移動している向きの方向を負とするとき、この自動車の速さはいくらになるでしょうか。
解答1
上の速度と速さの定義を用います。
速さは向きがないスカラー量(大きさのみあり)であるため、絶対値をとればよく速さ80km/hと変換できます。
続いて、もう一題は速さと速度に関係する問題を解いてみましょう。
例題2
ある人がランニングコースを秒速2mで走っています。今移動している向きの方向を正とするとき、この人の速度はいくらになるでしょうか。
解答2
速度であるため、大きさだけでなく、その向きも考慮していきます。
よって、この人の速度は+2m/sと求めることができるのです。なお、このときの速さであれば、2m/sと符号を省略してもいいです。
きちんと速度と速さの違いについて理解しておきましょう
まとめ
ここでは、速さと速度の定義やその違いについて解説していきました。
速さも速度も、「移動距離÷かかった時間」と表現できる似ている物理量といえます。
ただ、速度には大きさと向きがある量であるのに対して、速さとは大きさのみの量と違いがあります。よって、速さは速度の絶対値と考えるといいです。
なお、速度を表すときには大きさだけでなく、符号(向き)も表示させ、速さは大きさのみを記載するのが、違いです。
速度と速さの違いを理解して、コミュニケーションをより充実させていきましょう。