よく算数や数学において、図形中の線分の長さを計算する場面が多くでてきます。
特に、立体図形ではさまざまな特徴があるため、問題として出題される場合が多いです。例えば、立方体の対角線の長さを辺の長さから計算するときには、どのように対処するといいのか理解していますか。
ここでは、立方体における辺の長さと対角線の長さの変換方法について解説していきます。
目次
立方体の長さの計算方法
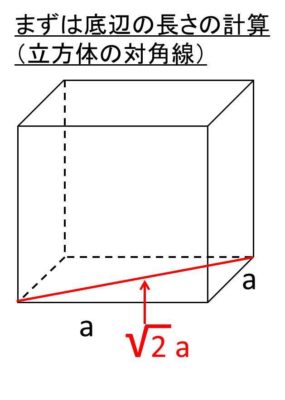
まず、立方体における対角線を図示すると以下の通りとなります。
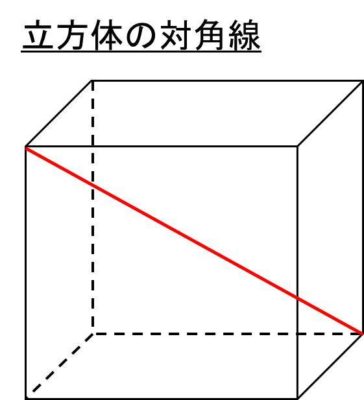
ここで立方体の対角線の長さを求めるためには、三平方の定理を2回使う必要があります。まずは、底辺となる底面の正方形の対角線の長さを求めていきましょう。
正方形の対角線の長さはこちらにても解説しているように、立方体の辺の長さをaとすると対角線の長さは√2aとなります。

よって、立方体の対角線の長さを求めるためには、この長さ√2aの辺を底辺、高さa、斜辺からできる直角三角形に対して、再び三平方の定義を適用していきます。
立方体の対角線の長さ=√(√2a^2 + a^2)と求めることができるわけです。具体的に計算していくと、立方体の対角線の長さ=√(2a^2 + a^2)=√3a と求められます。
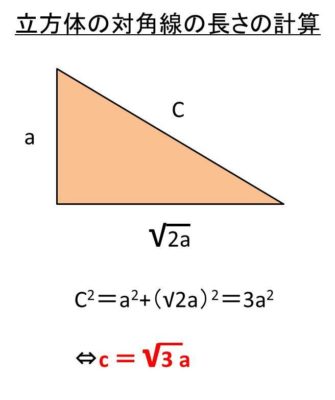
これが立方体における対角線を算出する方法となります。
なお、正方形における対角線の長さを求める方法はこちらに記載していますので参考にしてみてください。
立方体の対角線の長さを求める計算問題を解いてみよう
それでは、立方体における辺の長さから対角線の長さに変換する方法に慣れるためにも、実際の数値を用いて練習問題を解いていきましょう。
例題1
ある立法体の辺の長さは3cmです。この立方体における対角線の長さを求めていきましょう。
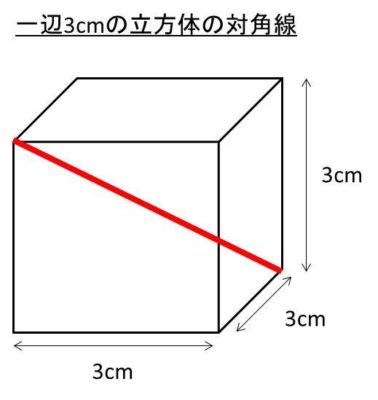
解答1
上の公式を適用します。よって、対角線の長さ=√3 ×3 = 1.732 × 3 = 5.196 となります。
続いて、もう一題立方体の対角線の長さの演習問題にチャレンジしていきましょう。
問題2
ある立方体の一辺の長さは6cmです。この立方体における対角線の長さを求めていきましょう。
解答2
こちらも上の公式を基に計算していきましょう。なお、イメージしにくいときは、上のよう立体図形を実際に書いてみるといいです。
そして立方体の対角線の長さは√3× 6 = 1.732 × 6 = 10.392 と算出されるのです。
なお、この公式自体を忘れたとしても、導出できるようにしておくといいです。詳しい手順を以下で確認してます。
まずは、底面の対角線を考えます。ここは正方形の対角線に相当するため √2 × 6が底辺の長さとなるわけです。
さらに、三平方の定理を利用しましょう。すると、立方体の対角線の長さ=√(6^2 + (√2 × 6)^2 )=√(36 + 72)=√96 = 6√3と上の計算と一致することがわかります。
まとめ
ここでは、立方体のの辺の長さから対角線の長さに変換する方法について解説しました。
立方体において対角線の長さを計算するためには、まず底面の対角線の長さを三平方の定理を用いて、計算します。その上で再度「立方体の対角線、辺(高さ)、底辺」にて三平方の定理を使用し求めていきましょう。
詳しい計算過程は上述の通りですが、結果は√3a(aは立方体の辺の長さ)となることを理解しておきましょう。さらに、この公式を忘れたとき、思い出せるように導出過程もきちんと理解しておきましょう。
立方体での対角線の長さを求める方法を理解し、より算数・数学的な処理を楽しんでいきましょう。