算数、数学を学んでいるときにさまざまな種類の比について考えることがあります。
例えば、立体図形であれば、相似比、面積比(表面積の比)、体積比などが挙げられます。これらの比は状況に応じて使い分ける必要があり、各々相互変換できるようにしておくといいです。
ここでは、特に円錐や三角錐などの体積比を計算する方法について確認していきます。
目次
円錐の体積比を相似比(辺の長さの比)から求める方法
まずは、代表的な立体図形である円錐(えんすい)について考えていきます。
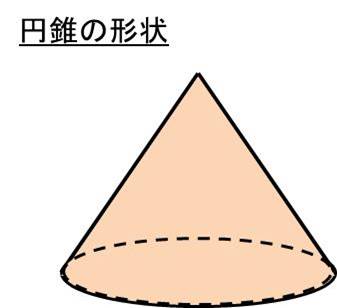
円錐とは以下のように、底面が円であり、先端が一点で交わった頂点となっている図形のことを指します。
ここである相似比(辺の長さの比)がa:bである円錐を考え、このときの体積比を考えていきましょう。
まずは、底面の比(面積比)を考えていきます。
円の面積は半径×半径×3.14(円周率)で求めることができるため、辺の長さの比でa:bであれば、面積比はa×a:b×b =a^2:b^2と換算できるのです。
さらに、体積は底面積×高さで求めることができるため、このa2:b2に対して、さらに各々の相似比をかけたものがこれに相当します。
よって、相似比がa:bの円錐の体積比=a2×a:b2×b=a^3:b^3と求めることができました。

つまり、辺の長さの比(相似比)の3乗の比が体積比に相当することを理解しておきましょう。
円錐の体積比の計算問題を解いてみよう
それでは、塩水の相似比、面積比、体積比の算出に慣れるためにも、練習問題を解いていきましょう。
例題
辺の長さの比(相似比)が3:2である円錐の体積比はいくつになるでしょうか。
解答
上の計算式を利用していきます。
相似比の3乗を行えばいいため、3×3×3:2×2×2=27:8と求めることができるのです。
それでは逆に、円錐における体積比から相似比への換算も行ってみましょう。
例題2
ある相似な円錐の体積比は、125:64ででした。この図形の辺の長さの比はいくらになるでしょうか。
解答2
今度は3乗するのではなく、逆に3乗根(1/3乗)をとっていきます。
このとき、5の3乗が125、4の3乗が64であるため、この円錐の相似比は5:4と変換できるのです。
三角錐の体積比の計算方法
今度は、三角錐において、相似比や面積比から体積比に換算する方法について解説していきます。
円錐同様に、三角錐での底面積を相似比から算出していきましょう。
すると、底面積=底辺×高さ÷2で算出でき、÷2は相似比との関係がないことから、三角錐であっても各々の2乗が面積比となるわけです。
辺の長さの比がc:dの円錐であれば、c^2:d^2が面積の比となるのです。
さらに三角錐の体積を考えるのであれば、円錐と同様に底面積に高さをかける必要があります。
よって、体積比は三角錐も円錐と同様であり、相似比を3乗したものがこれに相当するわけです。つまり、c^3:d^3が三角錐の体積比と考えるといいです。

このように相似な立体の体積比は、どのような形状であっても辺の長さの比の3乗に相当します。立体の体積の単位にm3(立法メートル)などと長さの単位のmを3乗したものを使用することと併せて、このことを理解しておくといいです。
三角推の体積比の練習問題を解いてみよう
それでは、実際の数値を基に、三角錐において辺の長さの比と体積比を換算する方法について確認していきます。
例題
ある相似比2:7の三角錐では、体積比はいくつになるでしょうか。
解答
上述のように、体積比の求め方は辺の長さの比を3乗すればいいので、2^3:7^3=8:343と変換されました。
今度は逆に体積比から辺の長さの比を求めていきましょう
例題
ある相似な三角錐二つの体積比は、1:27です。このときの、二つの立体図形の相似比はいくらになるでしょうか。
解答
こちらでも、体積比を求めるには3乗根をとるといいです。
具体的には3の3乗が27であるため、辺の長さの比は1:3となります。
きちんと理解しておきましょう。