数学の勉強をしていると、平方根の計算に出会うことがよくあります。特に289の平方根は、計算問題や応用問題で頻繁に登場する重要な数値です。一見すると難しそうに見えるかもしれませんが、実は289の平方根には面白い特徴があり、覚えやすい方法も存在するのです。
この記事では、289の平方根の正確な値から近似値、さらには実践的な計算方法まで詳しく解説していきます。語呂合わせを使った記憶術や、簡単に計算できるテクニックもご紹介しますので、数学が苦手な方でも安心して読み進めていただけるでしょう。それでは早速、289の平方根について詳しく見ていきましょう。
目次
289の平方根の値はいくつか
それではまず、289の平方根の正確な値について解説していきます。
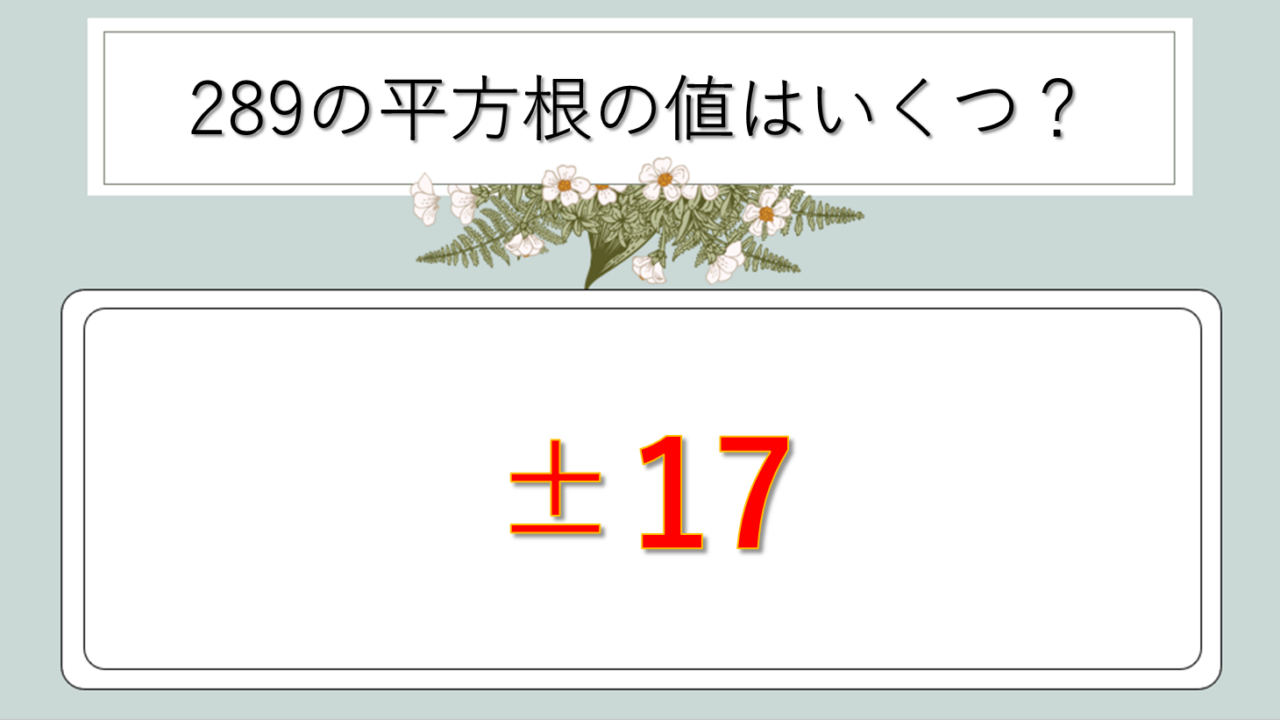
289の平方根は17です。これは整数値として表すことができる、いわゆる「完全平方数」の平方根なのです。
√289 = 17
確認:17 × 17 = 289
完全平方数とは、ある整数を2乗した結果得られる数のこと。289は17の2乗なので、その平方根は綺麗に17という整数になります。これは数学において非常に扱いやすい性質ですね。

実際に検算してみると、17×17=289となり、確かに正しいことが分かるでしょう。このように整数で割り切れる平方根は計算がシンプルで、様々な問題で活用されます。
【例】289の平方根を使った計算
√289 + √289 = 17 + 17 = 34
2√289 = 2 × 17 = 34
ちなみに、平方根には正の値と負の値の2つが存在します。厳密には±17が答えとなりますが、一般的に√の記号を使う場合は正の値である17を指すことが多いです。
289の平方根の覚え方と語呂合わせ
続いては、289の平方根を効率的に記憶する方法を確認していきます。
数学の勉強では、重要な数値を暗記しておくと計算スピードが格段に上がります。289の平方根である17を覚えるための語呂合わせをいくつかご紹介しましょう。
語呂合わせの例
「肉屋(289)でイイナ(17)」
という語呂合わせが分かりやすいですね。肉屋の289という数字から、イイナ(17)を連想する方法です。
他にも「ニワトリハク(289)、イーナ(17)」といった覚え方もあります。自分なりにストーリーを作って覚えると、より記憶に定着しやすいでしょう。
【語呂合わせ一覧】
・肉屋(289)でイイナ(17)
・ニワトリハク(289)、イーナ(17)
・ニッパク(289)は一七(17)
パターン認識による覚え方
語呂合わせ以外にも、数字のパターンで覚える方法があります。17という数字は10の位と1の位を足すと8になり、289の百の位である2と合わせると「2-8」という組み合わせになります。
また、17は素数であることも特徴的です。このような数学的な性質と結びつけて記憶すると、忘れにくくなるでしょう。
289の平方根の近似値について
続いては、289の平方根の近似値の考え方について見ていきます。
289の平方根は正確に17という整数値なので、実は近似値を考える必要はありません。しかし、平方根の概念を理解するために、近似値の求め方を知っておくことは有意義です。
小数点以下の確認
289の平方根を小数で表すと、17.000000…となり、小数点以下はすべて0が続きます。これは完全平方数の特徴ですね。
√289 = 17.0(小数点以下はすべて0)
仮に288や290といった289に近い数の平方根を求める場合は、近似値が必要になります。比較のために見てみましょう。
| 数値 | 平方根 | 近似値(小数第2位まで) |
|---|---|---|
| 288 | √288 | 16.97 |
| 289 | √289 | 17.00 |
| 290 | √290 | 17.03 |
この表からも分かるように、289だけが綺麗に整数値になっているのです。
電卓での確認方法
実際に電卓で√289を計算してみると、17とそのまま表示されます。これは計算ミスの確認にも使えるでしょう。電卓によっては「17.」や「17.0」と表示されることもありますが、いずれも同じ意味です。
289の平方根の計算方法
続いては、289の平方根を実際に計算する方法を確認していきます。
平方根を求める方法はいくつかありますが、ここでは代表的な3つの方法をご紹介しましょう。
素因数分解を使った方法
最も確実な方法は素因数分解を利用することです。289を素因数分解してみましょう。
【素因数分解の手順】
289 ÷ 17 = 17
17 ÷ 17 = 1
したがって、289 = 17 × 17 = 17²
よって、√289 = 17
この方法なら確実に答えを導き出せます。ただし、289が17で割り切れることに気づく必要があるのが難点ですね。
推測と検算による方法
平方根の値をある程度推測してから、実際に2乗して確認する方法もあります。
まず、289に近い完全平方数を考えてみましょう。16² = 256、20² = 400なので、√289は16と20の間にあることが分かります。
【推測の過程】
15² = 225(小さすぎる)
16² = 256(まだ小さい)
17² = 289(これだ!)
このように順番に試していけば、17にたどり着けるでしょう。
筆算による開平法
昔ながらの方法として、筆算で平方根を求める「開平法」という技術もあります。現代ではあまり使われませんが、電卓がない状況では有効な手段です。
開平法は複雑な手順を踏むため、ここでは詳細は省略しますが、2桁ずつ区切って計算を進めていく方法となります。興味のある方は専門書などで調べてみると良いでしょう。
289を簡単にする方法
続いては、289という数を様々な形で簡単に表現する方法を見ていきます。
289の因数分解
289は先ほども触れたように、17の2乗です。これが最もシンプルな表現でしょう。
289 = 17²
17は素数なので、これ以上因数分解することはできません。素数とは1とその数自身以外に約数を持たない数のことですね。
289に関連する数学的性質
289には面白い性質がいくつかあります。例えば、連続する整数の和で表すこともできるのです。
| 表現方法 | 計算式 |
|---|---|
| 2乗 | 17² |
| 奇数の和 | 1+3+5+7+…+33(17個の奇数) |
| 素因数分解 | 17 × 17 |
奇数を順番に足していくと平方数になるという性質は、数学の美しさを感じさせてくれます。
ルート記号での表現
√289という形で表現されている場合、これを簡単にすると単に17となります。ルートの中身が完全平方数なら、ルートを外せるのです。
【ルートの簡略化】
√289 = √(17²) = 17
2√289 = 2 × 17 = 34
√289 × √289 = 17 × 17 = 289
このように、ルートを外せるかどうかを判断することは、数式を簡単にする上で非常に重要です。
289の平方根を使った応用問題
最後に、289の平方根を実際の問題でどう活用するかを確認していきます。
面積から辺の長さを求める問題
正方形の面積が289cm²のとき、一辺の長さは何cmでしょうか。これは√289を求める問題ですね。
【問題】正方形の面積が289cm²のとき、一辺の長さは?
【解答】一辺 = √289 = 17cm
このように、実生活での図形問題でも平方根の知識は活躍します。
三平方の定理での応用
直角三角形の2辺の長さが分かっているとき、残りの1辺を求める際に平方根を使います。
例えば、直角を挟む2辺がそれぞれ8と15の直角三角形の斜辺の長さを求めてみましょう。
【三平方の定理の応用】
斜辺² = 8² + 15²
斜辺² = 64 + 225 = 289
斜辺 = √289 = 17
このように、289の平方根が17であることを知っていれば、素早く答えにたどり着けるでしょう。
二次方程式での利用
二次方程式を解く際にも平方根の知識が必要です。例えば、x² = 289という方程式を解いてみましょう。
x² = 289
x = ±√289 = ±17
答え:x = 17 または x = -17
平方根には正負2つの値があることを忘れてはいけません。問題文の条件によって、正の値だけを答える場合もあれば、両方を答える場合もあります。
まとめ 289の平方根は17
289の平方根について、値から計算方法、覚え方まで幅広く解説してきました。√289 = 17という綺麗な整数値になることが、この数の最大の特徴です。
語呂合わせでは「肉屋(289)でイイナ(17)」といった方法が使えますし、素因数分解や推測と検算による計算方法も実践的でしょう。289は17²という形で簡単にでき、これは完全平方数ならではの性質となります。
実際の数学の問題では、面積計算や三平方の定理、二次方程式など様々な場面で活用される重要な知識です。しっかりと理解して、計算力の向上に役立ててください。