169の平方根の値はいくつ？覚え方や近似値や計算方法は？語呂合わせも【簡単にすると？】

数学の勉強をしていると、平方根の計算に出会う機会は多いもの。特に169という数字は、平方根を考える上で非常に重要な数値なのです。169の平方根を求めることは、数学の基礎力を測る良い指標にもなるでしょう。

平方根とは、ある数を2乗するともとの数になる値のことを指します。つまり、169の平方根とは「2乗すると169になる数」ということ。この記事では、169の平方根の値や覚え方、計算方法について詳しく解説していきますね。さらに、実生活での応用例や、似た数値との比較なども紹介します。

平方根の理解は、中学数学だけでなく高校数学、さらには実生活の様々な場面で役立つ知識です。建築や設計、物理計算など、幅広い分野で活用されているため、しっかりと身につけておきたいところ。

それでは、まず169の平方根の具体的な値について解説していきます。

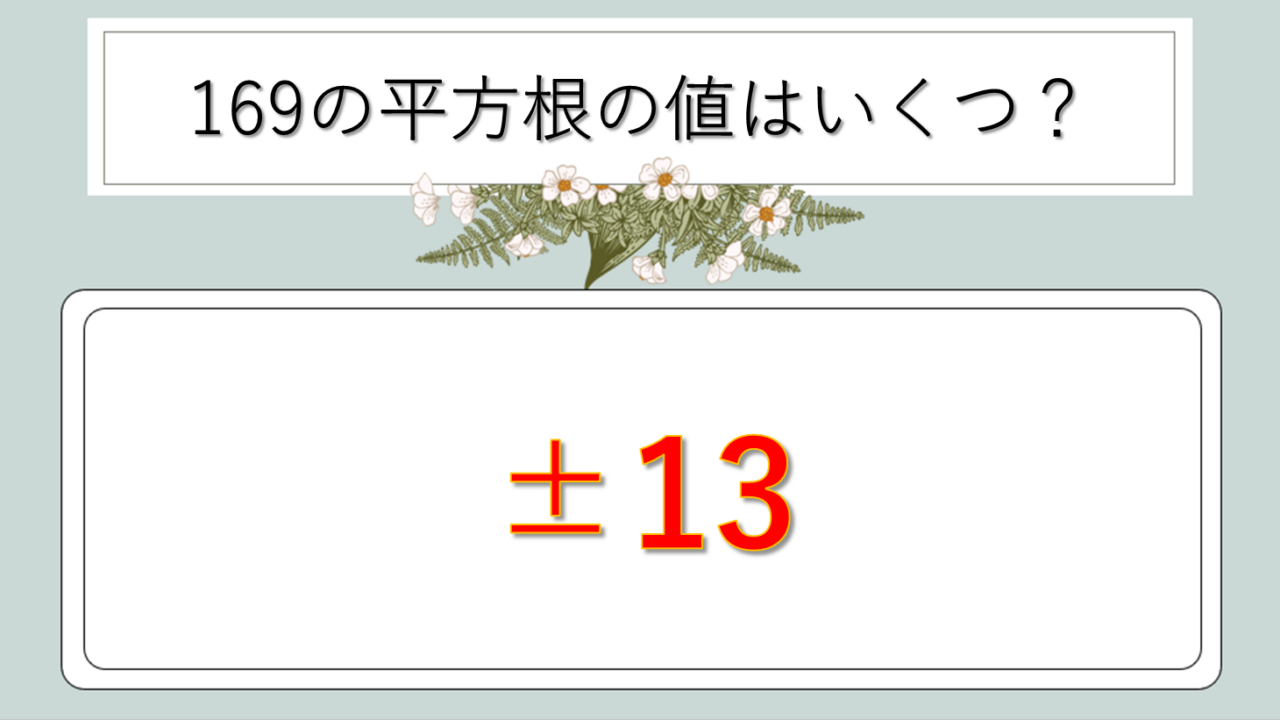
169の平方根の値はいくつ？

なぜなら、13×13=169となるから。これは平方根の中でも特に覚えやすい値の一つでしょう。

ただし、厳密に言えば平方根には正と負の2つの値が存在します。

通常、√記号を使う場合は正の平方根のみを指すことが多いですが、方程式を解く際などには両方の解を考える必要があるんです。

169は完全平方数と呼ばれる特別な整数。完全平方数とは、整数の2乗で表せる数のことを指します。1、4、9、16、25、36…と続く数列の一つですね。

13という数字は素数であり、169=13²という関係性から、素因数分解すると13×13となります。この性質により、169の平方根は非常にシンプルな整数値になるわけです。

169の平方根の覚え方は？語呂合わせも紹介

続いては、169の平方根を効率よく記憶する方法を確認していきます。

数学の学習において、暗記は必ずしも必要ではありませんが、よく使う値は覚えておくと計算がスムーズになるもの。169の平方根=13という関係は、いくつかの方法で記憶できるでしょう。

数字の並びで覚える方法

「1・6・9」と「1・3」の関係

に注目してみましょう。169という3桁の数と、その平方根13という2桁の数。どちらも1から始まるという共通点がありますね。

また、169を分解すると「100+69」となり、13²=169という計算を何度か繰り返すことで自然と記憶に定着していきます。

語呂合わせで覚える

語呂合わせは人によって合う合わないがありますが、音のリズムで覚える方法は記憶の定着に効果的でしょう。

周辺の平方数との関連で覚える

以下の表で、169の前後の完全平方数を確認してみましょう。

数値	平方根	計算式
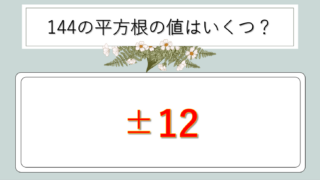
144	12	12×12=144
169	13	13×13=169
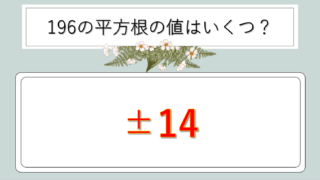
196	14	14×14=196
225	15	15×15=225

このように系列で覚えると、前後の数値との関連性から記憶しやすくなります。12²=144、13²=169、14²=196という流れで覚えておくと良いでしょう。

169の平方根の計算方法は？

では、実際に169の平方根を計算で求める方法について見ていきましょう。もし169という数値の平方根を知らなかった場合、どのように求めればよいのでしょうか。

素因数分解を使った方法

まず、素因数分解による求め方があります。

この方法は確実で理論的。素因数分解ができれば、平方根も自動的に求まるわけです。

試行錯誤による方法

169に近い完全平方数を探していく方法もあります。

範囲を絞り込んでいく

ことで、正解にたどり着けるでしょう。この方法は直感的で分かりやすいですね。

筆算による開平法

伝統的な計算方法として、開平法という手法も存在します。これは平方根を筆算で求める方法で、電卓がない時代には重宝されていました。ただし、169のような簡単な完全平方数の場合は、素因数分解や試行錯誤の方が効率的でしょう。

169の平方根を簡単にすると？

「169の平方根を簡単にする」という表現について考えてみます。

なぜなら、13は既に最もシンプルな形だから。平方根の簡単化とは、通常√の中を可能な限り小さくする作業を指します。

しかし169の場合は、√169=13と完全に根号が外れてしまうため、これが最終的な答え。これ以上の簡単化は不要なんです。

平方根の簡単化における重要なポイントは、完全平方数を因数として見つけ出すことでしょう。169は13²という完全平方数そのものなので、√を外して整数13になるわけですね。

169の平方根の近似値について

続いては、近似値という観点から169の平方根を確認していきます。

169の平方根は13という整数値ですから、実は近似値を考える必要はありません。正確な値そのものが整数なのです。

しかし、計算機を使わずに平方根を概算する技術は、他の数値でも役立つため、ここで学んでおく価値があるでしょう。

近似値が必要になるケース

このように、完全平方数でない数値の平方根を求める際に近似の考え方が重要になってきます。

小数点以下の精度

√169 = 13.000000…と、小数点以下は全て0が続く形。計算機で確認しても、13ちょうどという値が得られるはずです。

以下の表で、169周辺の数値の平方根を比較してみましょう。

数値	平方根(正確な値または近似値)	小数点以下
168	12.961…	あり
169	13.000	なし
170	13.038…	あり

169だけが完全な整数値

を持つことが分かりますね。

169の平方根の実生活での応用

数学の知識は、実際の生活でどう役立つのでしょうか。169の平方根=13という関係も、様々な場面で活用されています。

正方形の面積計算

建築や造園の分野

では、このような計算が頻繁に必要になるもの。面積から一辺の長さを逆算する際に平方根を使うわけですね。

ピタゴラスの定理での活用

直角三角形において、斜辺の長さを求める際にも平方根が登場します。

これは有名な「5:12:13」の直角三角形として知られており、建築現場などで直角を作る際の基準としても使われています。

統計学での標準偏差計算

データ分析の分野でも平方根は欠かせません。分散から標準偏差を求める際、平方根の計算が必要になるんです。もし分散が169であれば、標準偏差は13となるでしょう。

関連する平方根との比較

169の平方根をより深く理解するため、関連する数値と比較してみます。

2乗すると169になる数の特徴

13という数は素数。素数を2乗した数の平方根は、常にその素数自身になります。

素数	2乗した値	平方根
7	49	7
11	121	11
13	169	13
17	289	17

素数の2乗は覚えやすい

という特徴があります。13²=169もその一つですね。

100番台の完全平方数

100から200の間にある完全平方数は限られています。

このように、100番台の完全平方数は4つだけ。その中の一つが169なのです。

まとめ：169の平方根は13

この記事では、169の平方根について様々な角度から解説してきました。13×13=169という関係は、数学の基本として覚えておきたい知識の一つでしょう。

覚え方としては、語呂合わせ「いろくのルートはひとさん」や、前後の完全平方数(144、196)との関連で記憶する方法が効果的。計算方法としては、素因数分解や試行錯誤による方法があります。

実生活では、正方形の一辺の長さを求める計算や、ピタゴラスの定理での活用、統計計算など、様々な場面で役立つ知識なんです。特に5:12:13の直角三角形は、実用的な比率として建築現場などでも使われていますね。

169は完全平方数であり、その平方根13は整数値。近似値を考える必要がなく、これ以上簡単にすることもできません。この明快さこそが、169の平方根を学習する上での大きなメリットでしょう。

数学の基礎力を高めるため、13²=169という関係をしっかりと記憶し、様々な計算場面で活用していってください。