数学の学習において、平方根は避けて通れない重要な概念です。特に√40のような値は、入試問題や実生活の計算でも頻繁に登場するもの。しかし、ルート40と聞いて、すぐに正確な値や簡単な形を答えられる人は意外と少ないのではないでしょうか。
平方根の理解を深めることは、数学力の向上に直結します。今回は√40について、その正確な値から簡単にする方法、覚え方のコツ、さらには語呂合わせまで、徹底的に解説していきましょう。
計算が苦手な方でも理解できるよう、段階を追って丁寧に説明していきますので、ぜひ最後までお付き合いください。
目次
40の平方根の値はいくつか
それではまず、√40の具体的な値について解説していきます。
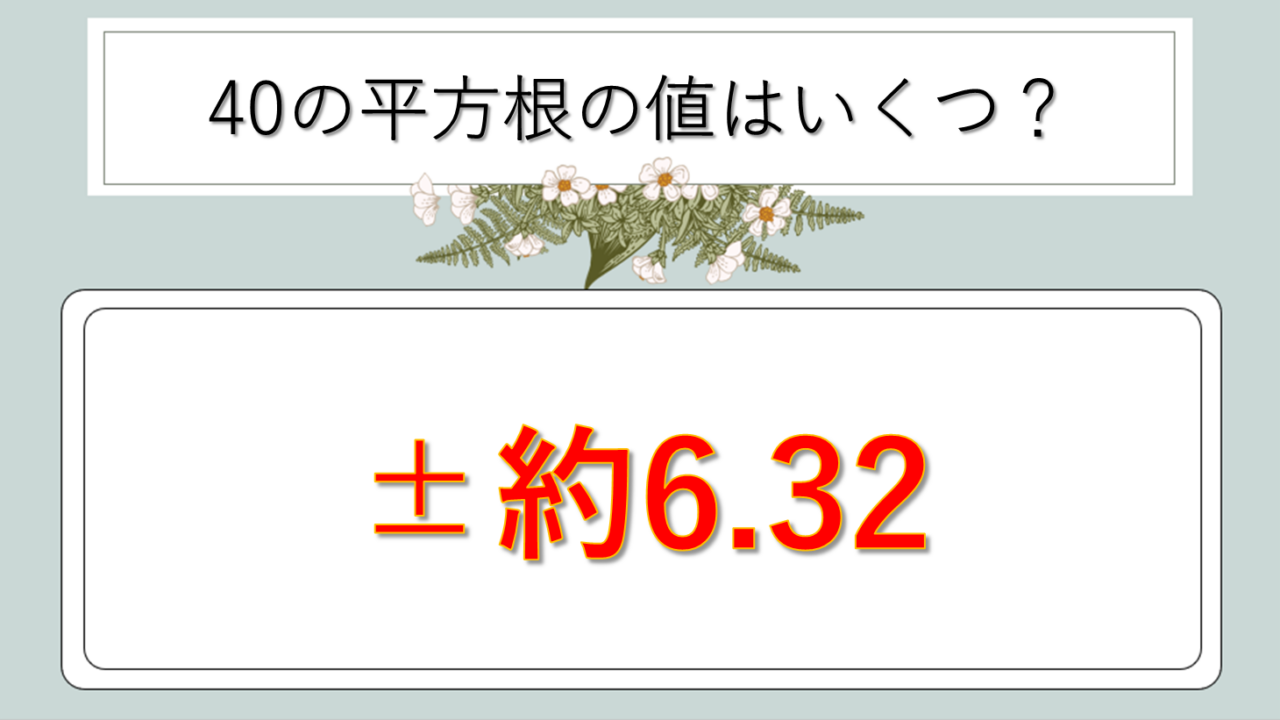
√40の正確な値は、約6.324555…となります。この値は無理数であり、小数点以下が永遠に続く数字です。日常的な計算では、小数第2位や第3位までの近似値を使用することが一般的でしょう。

電卓で計算すると6.32455532と表示されることが多く、これを四捨五入すれば様々な精度で扱えます。試験では小数第2位まで求められることが多いため、6.32という値を覚えておくと便利です。
√40 ≈ 6.324555320336759…
実用的には√40 ≈ 6.32と覚えましょう
ちなみに、√40は√36(=6)より大きく、√49(=7)より小さい値。この関係性を理解しておくと、計算結果の妥当性を確認する際に役立ちます。
40の平方根を簡単にする方法
続いては、√40をより扱いやすい形に変形する方法を確認していきます。
平方根を簡単にする基本は、根号の中の数を因数分解し、平方数を見つけ出すこと。40という数を素因数分解してみましょう。
40 = 2 × 2 × 2 × 5
40 = 4 × 10
ここで4は2²という平方数です。平方根の性質として、√(a×b) = √a × √bという関係があるため、これを利用します。
√40 = √(4×10)
√40 = √4 × √10
√40 = 2√10
したがって、√40を簡単にすると2√10
となります。この形が最もシンプルで、数学的に美しい表現でしょう。
なぜこの形が便利なのか。それは計算の際に扱いやすく、他の平方根との四則演算がスムーズになるからです。例えば√10との掛け算なら、2√10 × √10 = 2×10 = 20と簡単に計算できます。
| 表記 | 形式 | 用途 |
|---|---|---|
| √40 | 元の形 | 基本表記 |
| 2√10 | 簡単にした形 | 計算・代数的処理 |
| 6.32… | 小数形 | 実用計算・近似値 |
40の平方根の覚え方と語呂合わせ
続いては、√40の値を記憶するための効果的な方法を確認していきます。
数学の学習において、覚えるべき値は数多く存在しますが、語呂合わせは最も効果的な記憶術の一つ。√40 ≈ 6.32という値を覚えるための語呂合わせをいくつかご紹介しましょう。
「ろくさん(6.3)に(2)なる40」
「無事に(6.32)よかった40人」
また、2√10という簡単な形で覚える方が実践的かもしれません。「40は4×10だから、2√10」という流れで覚えると、計算の際にすぐ思い出せるでしょう。
さらに効果的な覚え方として、関連する平方根とセットで覚える方法があります。
| 平方根 | 簡単な形 | 近似値 |
|---|---|---|
| √10 | √10 | 3.16 |
| √20 | 2√5 | 4.47 |
| √40 | 2√10 | 6.32 |
| √80 | 4√5 | 8.94 |
この表から分かるように、√40は√10の2倍の関係。つまり√10 ≈ 3.16を知っていれば、その2倍で6.32と導き出せるわけです。
視覚的に覚える方法も有効でしょう。6と7の間、より6に近い値と捉えると、イメージしやすくなります。
40の平方根の計算方法
続いては、√40を実際に計算する様々な方法を確認していきます。
電卓がない状況で√40の近似値を求めたい場合、いくつかのアプローチが考えられます。最も基本的なのは、平方数を利用した挟み込み法でしょう。
6² = 36
7² = 49
36 < 40 < 49 より、6 < √40 < 7
さらに精度を上げるには、6.3や6.4で試してみます。
6.3² = 39.69
6.4² = 40.96
39.69 < 40 < 40.96 より、6.3 < √40 < 6.4
40に最も近いのは39.69なので、√40 ≈ 6.3と分かります。さらに細かく求めるなら、6.32²を計算してみましょう。
6.32² = 39.9424
6.33² = 40.0689
40に近いのは6.32の方。したがって√40 ≈ 6.32という近似値が得られます。
別の計算方法として、2√10の形を利用する手法もあります。√10 ≈ 3.162を知っていれば、単純に2倍して6.324と求められるわけです。
計算のコツ:√40 = 2√10を利用する
√10 ≈ 3.162 なので、2 × 3.162 = 6.324
筆算で平方根を求める開平法という古典的手法もありますが、現代では実用的ではないかもしれません。しかし、原理を理解することは数学的思考力を養うのに役立つでしょう。
40の平方根を使った実践問題
続いては、√40を実際に使う問題例を確認していきます。
数学の試験や実生活で、平方根の知識はどのように活用されるのか。具体例を見ていきましょう。
問題1:√40 + √10 を簡単にせよ
解答:√40 = 2√10 なので
2√10 + √10 = 3√10
このように、簡単な形に直しておくと計算がスムーズになります。同じ根号をまとめる際は、係数を足し算するだけ。
問題2:√40 × √5 を計算せよ
解答:√40 × √5 = √(40×5) = √200
√200 = √(100×2) = 10√2
平方根同士の掛け算は、根号の中を掛け算してから簡単にするのが基本でしょう。
実生活での応用例も見てみましょう。面積が40㎡の正方形の土地があるとします。この一辺の長さはいくつか。
一辺の長さ = √40 = 2√10 ≈ 6.32m
つまり、約6.32メートル四方の正方形ということになります。
さらに複雑な問題も考えてみましょう。
問題3:√40の値を有理化せよ(分母に含まれる場合)
例:10/√40 を有理化すると
10/√40 = 10/(2√10) = 5/√10
= 5√10/10 = √10/2
有理化の過程で√40を2√10に変形することで、計算が格段に楽になります。
| 計算の種類 | ポイント |
|---|---|
| 加法・減法 | 2√10の形にして係数を計算 |
| 乗法 | 根号内を掛けてから簡単化 |
| 除法 | 有理化を忘れずに |
| 近似計算 | 6.32を使用 |
40の平方根と関連する数学知識
最後に、√40に関連する数学的な知識を確認していきます。
平方根の理解を深めるには、周辺知識も同時に身につけることが重要。√40を学ぶことで、他の概念も理解できるようになるでしょう。
まず、平方根の定義について確認しましょう。√40とは、2乗すると40になる正の数のこと。数学的には、(√40)² = 40という関係が成り立ちます。
平方根の基本性質
√(a×b) = √a × √b
√(a÷b) = √a ÷ √b
(√a)² = a
これらの性質を理解していれば、√40 = √(4×10) = 2√10という変形も自然に導けます。
40という数の数学的な特徴も興味深いものがあります。40 = 2³ × 5という素因数分解から、8と5の最小公倍数でもあるわけです。
平方根の大小関係も重要な概念でしょう。
√36 < √40 < √49
6 < 2√10 < 7
このような不等式は、解の範囲を絞り込む際に非常に有用。特に方程式を解く場合、おおよその値を推定できることは大きな強みとなります。
また、√40を含む二次方程式についても触れておきましょう。
x² = 40 の解は x = ±√40 = ±2√10
つまり x = 2√10 または x = -2√10
負の平方根も存在することを忘れてはなりません。ただし√40と表記する場合は、通常は正の値のみを指します。
数学的な美しさという観点から見ると、2√10という形は非常に洗練されています。係数2と根号内の10という組み合わせが、計算の見通しを良くしてくれるのです。
三平方の定理との関連も考えてみましょう。2と6を2辺とする直角三角形の斜辺は√40になります。
2² + 6² = 4 + 36 = 40
斜辺 = √40 = 2√10
このように、√40は幾何学的な意味も持っているのです。実際の図形問題でも頻出する値と言えるでしょう。
まとめ 40の平方根の値は
この記事では、40の平方根について様々な角度から解説してきました。
最後に、√40の学習を通じて身につくスキルについて整理しておきましょう。
因数分解の力、平方数の見極め、根号の性質の理解、近似値の計算能力など、数学の基礎体力が総合的に鍛えられます。
これらの知識は、より高度な数学を学ぶ際の土台となるもの。√40という一つの値から、これだけ多くの学びが得られるのですから、数学の奥深さを感じずにはいられません。
平方根の計算に慣れることで、数学全体への理解が深まり、問題解決能力も向上していくはず。日々の練習を重ねることで、自然と身についていくでしょう。